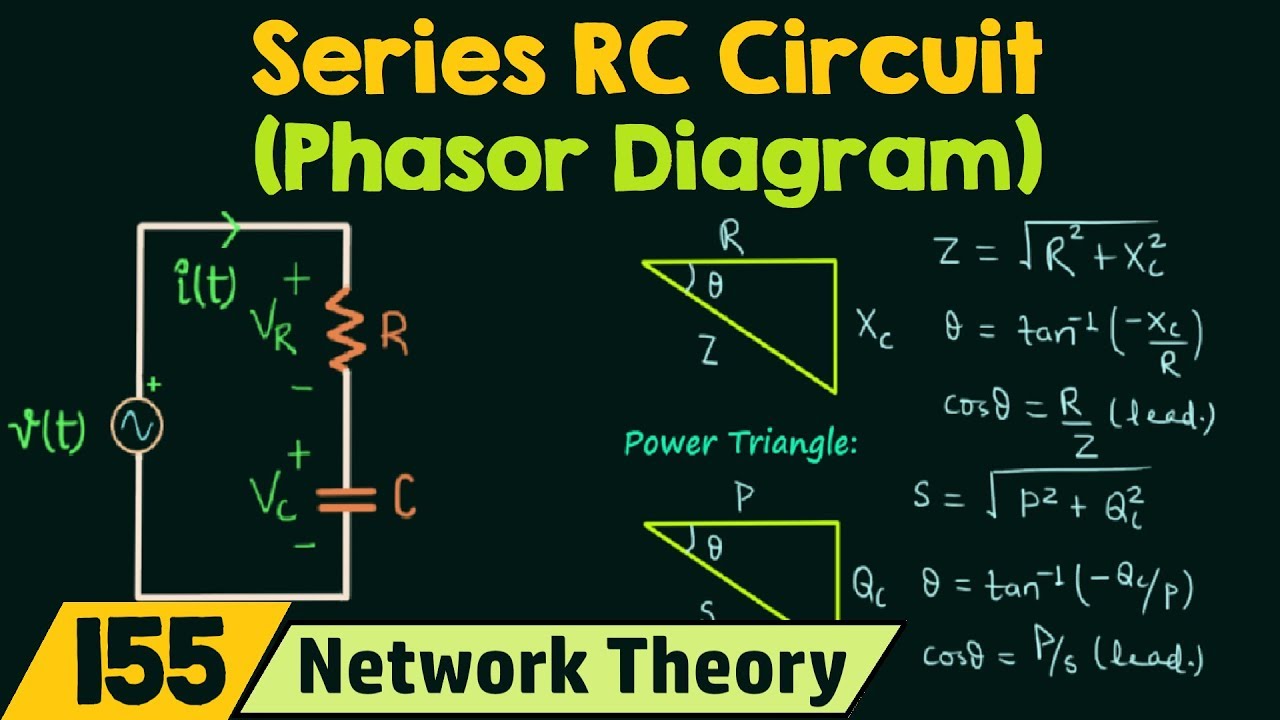
Unlocking AC Circuits: The Magic of LR Circuit Phasor Diagrams
Ever stare at an AC circuit and feel like you’re deciphering hieroglyphics? Alternating current, with its constantly fluctuating voltages and currents, can be a real head-scratcher. But what if there was a visual key, a secret decoder ring for understanding these complex electrical puzzles? Enter the phasor diagram for LR circuits, a powerful tool that transforms confusing sinusoidal waves into elegant, manageable vectors.
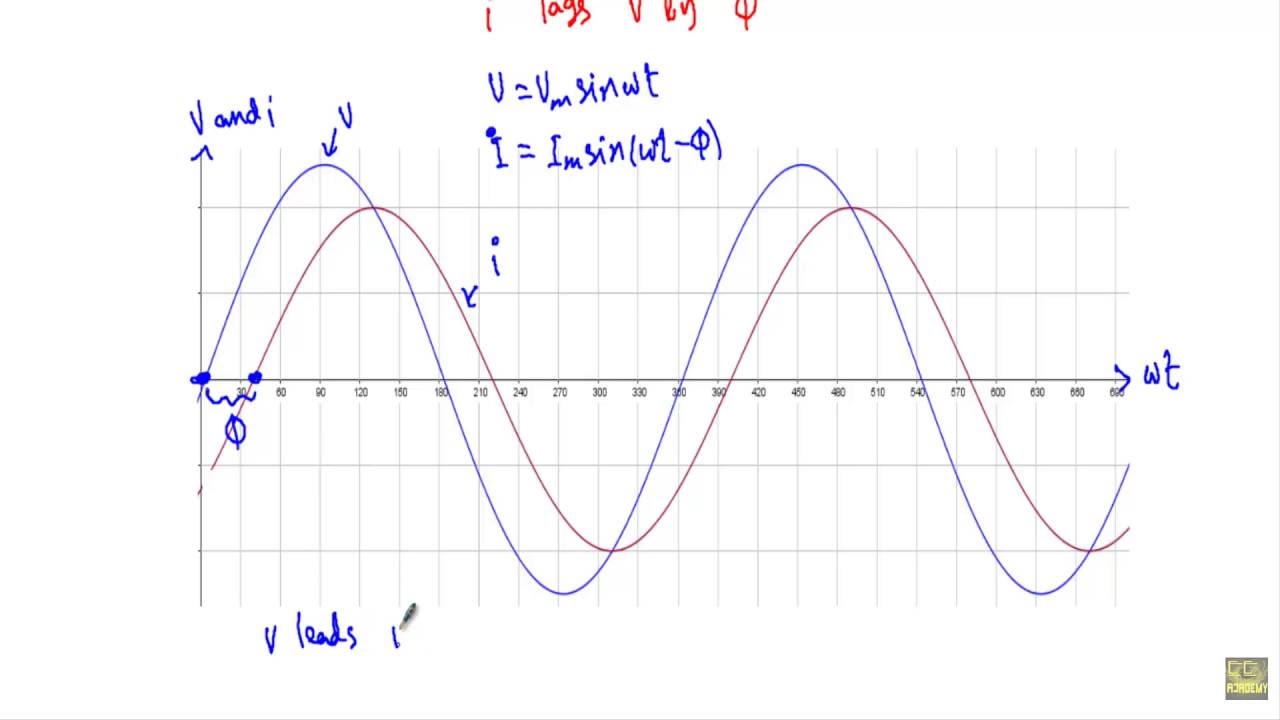
Imagine trying to add two constantly shifting quantities. It’s like trying to nail jelly to a wall. Now imagine freezing those quantities at specific moments, capturing their magnitude and direction. That’s the essence of a phasor. A phasor diagram for an LR circuit is a snapshot in time, representing the voltage and current as rotating vectors. This visual representation allows us to analyze the relationship between voltage and current in a way that’s far simpler than crunching trigonometric functions.
The concept of representing sinusoidal functions as rotating vectors arose from the need to simplify AC circuit analysis. Early electrical engineers grappled with complex equations involving sine and cosine functions. Phasor diagrams, rooted in vector mathematics, provided a much-needed visual and computational shortcut. Their development significantly advanced the understanding and design of AC circuits, paving the way for the power systems we rely on today.
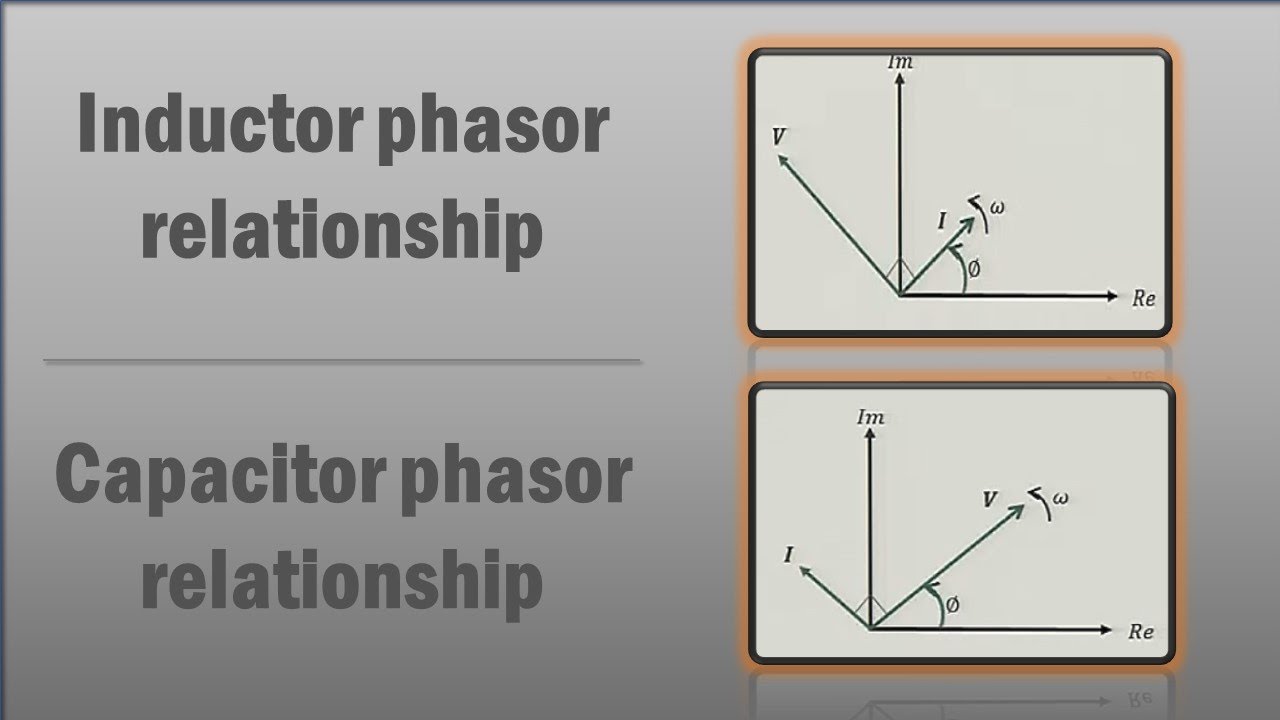
A phasor diagram for an LR circuit typically shows the voltage across the resistor (in phase with the current), the voltage across the inductor (leading the current by 90 degrees), and the total applied voltage. The lengths of these vectors represent the magnitudes of the voltages, and the angles between them represent the phase differences. This graphical representation makes it easy to see how the inductor's reactance affects the overall circuit behavior.
One of the primary challenges in analyzing LR circuits is understanding the phase relationship between voltage and current. Unlike purely resistive circuits, the presence of an inductor introduces a phase shift. The inductor's opposition to changes in current causes the current to lag behind the applied voltage. This phase difference is crucial for determining the circuit's impedance and power characteristics. Phasor diagrams vividly illustrate this phase shift, making it easier to grasp.
A simple example is a circuit with a resistor and inductor connected in series to an AC source. The current flowing through both components is the same. However, the voltage across the resistor is in phase with the current, while the voltage across the inductor leads the current. A phasor diagram clearly depicts this relationship, with the voltage phasor for the inductor 90 degrees ahead of the current phasor.
Benefits of phasor diagrams: 1) Simplified analysis: They transform complex equations into visual relationships. 2) Clear visualization: Phase relationships are easily seen. 3) Easier calculations: Vector addition simplifies impedance calculations.
Constructing a phasor diagram involves representing the current as a horizontal vector. The resistor voltage vector is also horizontal (in phase). The inductor voltage vector is drawn 90 degrees counterclockwise (leading). The total voltage is the vector sum of these two.
Advantages and Disadvantages of Phasor Diagrams
| Advantages | Disadvantages |
|---|---|
| Visual representation simplifies complex relationships | Only applicable to sinusoidal steady-state conditions |
| Facilitates easier calculations of impedance and other parameters | Can become complex for circuits with many components |
| Provides a clear understanding of phase relationships | Doesn't directly show transient behavior |
Best Practices: 1) Always use a consistent scale. 2) Clearly label all phasors. 3) Indicate the direction of rotation. 4) Choose a suitable reference phasor (usually current). 5) Verify your diagram against circuit calculations.
Real examples include analyzing the behavior of transformers, motors, and filters where understanding phase relationships is critical.
Challenges include dealing with complex circuits and non-sinusoidal waveforms. Solutions involve using software tools and advanced analysis techniques.
FAQ: 1) What is a phasor? 2) Why is the inductor voltage leading the current? 3) How do I calculate impedance using a phasor diagram? 4) What is the significance of the angle between voltage and current phasors? 5) Can phasor diagrams be used for DC circuits? 6) What are the limitations of phasor diagrams? 7) How do I construct a phasor diagram for a parallel LR circuit? 8) Where can I find more resources on phasor diagrams?
Tips: Always remember that phasors represent sinusoidal quantities at a specific frequency. Be mindful of the scale and units used in your diagram. Practice drawing phasor diagrams for different circuit configurations.
In conclusion, phasor diagrams are invaluable tools for anyone working with AC circuits. They provide a visual and intuitive way to understand the complex interplay of voltage, current, and impedance in LR circuits. Mastering this technique will equip you with a powerful skill for analyzing and designing AC circuits, opening up a world of understanding about the electrical systems that power our modern lives. By simplifying complex relationships into understandable visual representations, phasor diagrams empower us to tackle challenging circuit problems with confidence. So, embrace the power of phasor diagrams and unlock the secrets of AC circuits! Start exploring online resources, textbooks, and simulation software to deepen your understanding and put this powerful tool to practical use.
Unlock your tahoes towing power how much weight can it handle
Expressing love to mom printable i love you mom coloring pages
Buen viernes feliz fin de semana your guide to a happy weekend