Midsegments Of A Triangle Kuta
Triangles are one of the most fundamental shapes in geometry, and understanding their properties can lead to deeper insights into mathematics. One key concept related to triangles is the midsegments of a triangle, specifically in the context of Kuta. In this article, we will explore the history, definition, benefits, and practical applications of midsegments of a triangle Kuta.
History, Origin, Importance of Midsegments of a Triangle Kuta
The concept of midsegments in triangles has been studied for centuries, with roots in Euclidean geometry. In Kuta, a popular educational resource, the midsegments of a triangle play a crucial role in understanding triangle properties and relationships. By identifying and analyzing midsegments, students can gain a better grasp of geometric principles.
Definition, Explanation, and Simple Examples of Midsegments of a Triangle Kuta
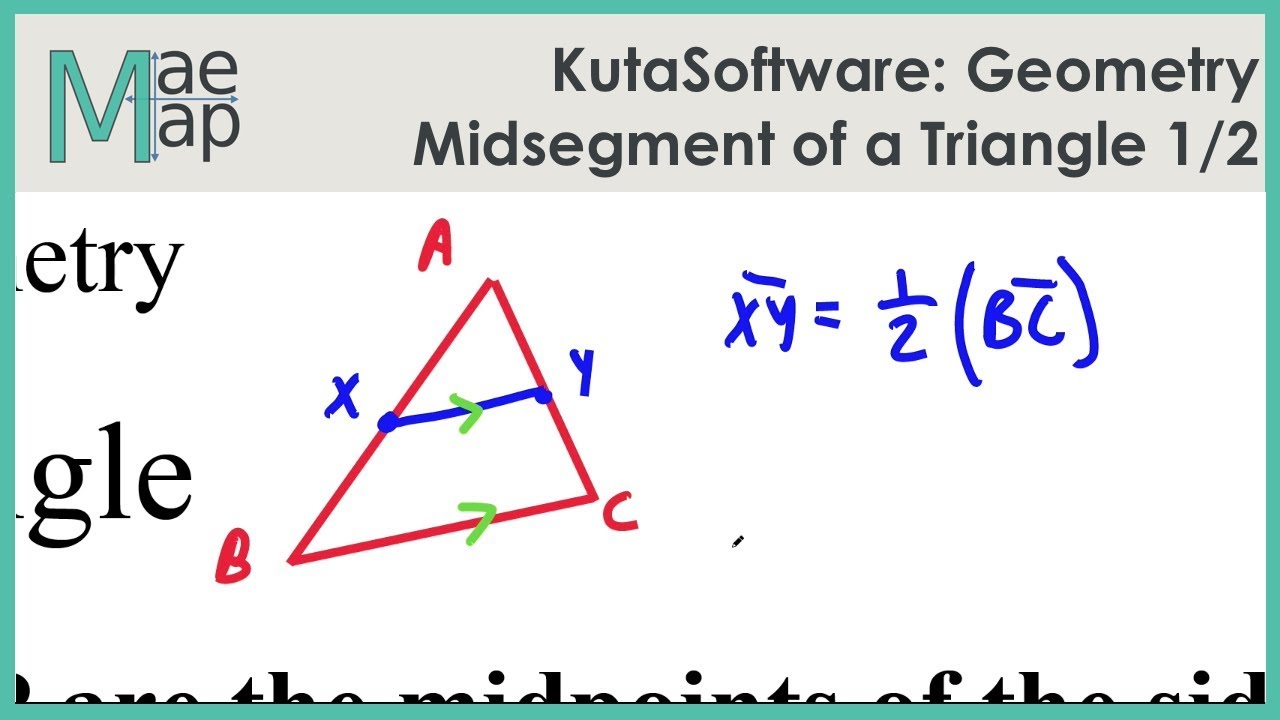
In geometry, a midsegment of a triangle is a line segment connecting the midpoints of two sides of a triangle. The midsegment is always parallel to the third side of the triangle and is half the length of that side. For example, in a triangle ABC, if D and E are the midpoints of sides AB and AC respectively, then DE is the midsegment parallel to BC.
Benefits of Midsegments of a Triangle Kuta
- Simplifies Triangle Analysis: By dissecting a triangle into midsegments, complex triangle properties become more manageable to study.
- Aid in Construction: Midsegments can be helpful in constructing various geometric shapes and designs.
- Enhances Problem-Solving Skills: Working with midsegments helps students develop critical thinking and problem-solving abilities.
Action Plan for Midsegments of a Triangle Kuta
One effective way to understand and utilize midsegments of a triangle in Kuta is to practice with interactive geometry software or worksheets provided by Kuta Software.
Checklist for Midsegments of a Triangle Kuta
- Identify the midpoints of two sides of the triangle
- Construct the midsegment between these midpoints
- Verify that the midsegment is parallel to the third side
Step-by-step Guide on Midsegments of a Triangle Kuta
- Identify the midpoints of two sides
- Connect the midpoints with a line segment
- Verify that the midsegment is parallel to the third side
Recommendations for Resources on Midsegments of a Triangle Kuta
For additional practice and explanations on midsegments in geometry, websites like Kuta Software and Khan Academy offer excellent resources for students.
Advantages and Disadvantages of Midsegments of a Triangle Kuta
- Advantage: Simplifies triangle analysis
- Disadvantage: Can be confusing for beginners
Best Practices for Implementing Midsegments of a Triangle Kuta
- Practice with various triangle types to strengthen understanding
- Use visualization tools to aid in studying midsegments
- Collaborate with peers to discuss and solve problems related to midsegments
Real-life Examples of Midsegments of a Triangle Kuta
- In architecture, midsegments help in designing structures based on triangular shapes.
- In engineering, understanding midsegments is crucial for constructing stable geometric forms.
- In art, midsegments can be used to create visually appealing patterns and designs.
Challenges and Solutions for Midsegments of a Triangle Kuta
- Challenge: Identifying midpoints accurately
- Solution: Use geometric tools to assist in locating midpoints
Questions and Answers for Midsegments of a Triangle Kuta
- What is the role of midsegments in studying triangles? Midsegments provide insights into the properties and relationships of triangles.
- How can midsegments be used in real-world applications? Midsegments are essential in various fields like architecture, engineering, and art.
- What are the benefits of understanding midsegments in geometry? Understanding midsegments enhances problem-solving skills and geometric reasoning.
Tips and Tricks for Midsegments of a Triangle Kuta
- Practice identifying midpoints regularly
- Work on geometry problems involving midsegments
- Seek assistance from online resources for additional support
Conclusion
In conclusion, midsegments of a triangle in Kuta are a valuable tool for understanding geometric principles and relationships. By mastering the concept of midsegments, students can deepen their knowledge of geometry and enhance their problem-solving skills. Incorporating midsegments into geometry studies can lead to a greater appreciation and comprehension of the mathematical world. So, let's delve into the world of midsegments of a triangle Kuta and unlock the beauty of geometric analysis!
Turning 65 the clock is ticking on your oas application
Dreaming of daybeds finding the perfect wrought iron gem
The weight of silence exploring family dynamics in six feet under season 1 episode 11
