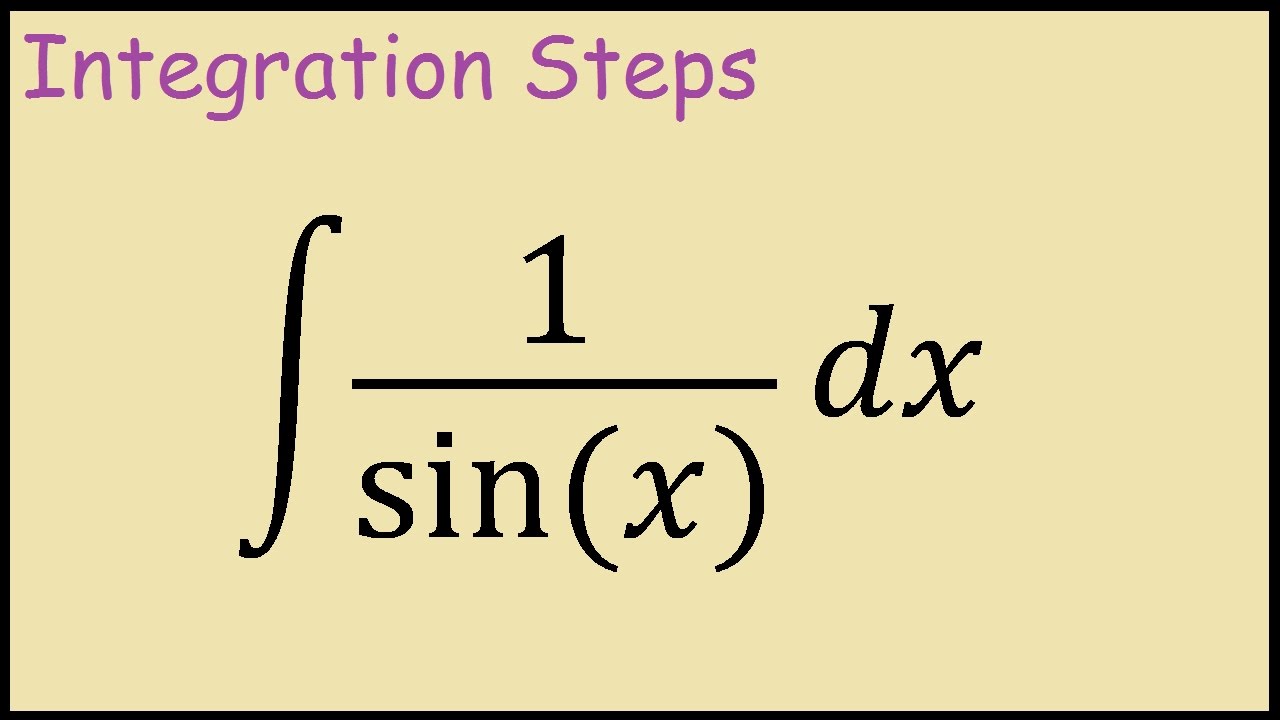Trigonometrische Integralen Ontrafeld: Een Diepgaande Blik op ∫ 1/(sin x - a sin x - b) dx
De wereld van de wiskunde is als een oneindige oceaan vol fascinerende geheimen, en trigonometrie is een van de meest intrigerende gebieden. Vandaag duiken we in de diepten van trigonometrische integralen en richten we onze aandacht op een specifiek type: ∫ 1/(sin x - a sin x - b) dx. Bereid je voor om meegenomen te worden op een reis vol wiskundige ontdekkingen!
Integralen, in essentie, stellen ons in staat om de oppervlakte onder een curve te berekenen, en trigonometrische integralen komen voor wanneer deze curven worden gedefinieerd door trigonometrische functies zoals sinus en cosinus. De integraal ∫ 1/(sin x - a sin x - b) dx, met zijn unieke structuur, vormt een interessante uitdaging die ons dwingt om onze trigonometrische vaardigheden en integratietechnieken aan te scherpen.
De geschiedenis van trigonometrische integralen is verweven met de ontwikkeling van de calculus zelf. Pioniers als Newton en Leibniz legden de basis voor dit vakgebied, en hun werk opende de deur naar het bestuderen van complexe integralen zoals degene die we hier onderzoeken.
Het belang van het begrijpen van integralen als ∫ 1/(sin x - a sin x - b) dx reikt verder dan de theoretische wereld van de wiskunde. Ze vinden toepassingen in diverse wetenschappelijke en technische disciplines, waaronder natuurkunde, engineering en informatica. Van het modelleren van periodieke verschijnselen tot het oplossen van differentiaalvergelijkingen, deze integralen spelen een cruciale rol in ons begrip van de wereld om ons heen.
Laten we, voordat we dieper ingaan op de specifieke technieken om ∫ 1/(sin x - a sin x - b) dx op te lossen, enkele belangrijke trigonometrische identiteiten en integratieregels herhalen die van pas zullen komen. Herinner je je de volgende identiteiten:
- sin^2(x) + cos^2(x) = 1 - 1 + tan^2(x) = sec^2(x)
Deze identiteiten stellen ons in staat om trigonometrische uitdrukkingen te vereenvoudigen en te manipuleren, wat cruciaal is bij het oplossen van integralen zoals ∫ 1/(sin x - a sin x - b) dx. Bovendien zullen integratietechnieken zoals substitutie en partiële breuken onmisbare instrumenten in ons arsenaal zijn.
Hoewel de specifieke stappen voor het oplossen van ∫ 1/(sin x - a sin x - b) dx afhangen van de waarden van a en b, omvat een algemene aanpak het gebruik van trigonometrische substitutie, gevolgd door algebraïsche manipulatie en de toepassing van partiële breuken. Deze aanpak stelt ons in staat om de integraal te vereenvoudigen tot een vorm die we direct kunnen oplossen met behulp van standaard integratieformules.
Naast het oplossen van ∫ 1/(sin x - a sin x - b) dx met de hand, zijn er tal van softwareprogramma's en online calculators die ons kunnen helpen bij het vinden van oplossingen voor trigonometrische integralen. Deze tools kunnen bijzonder nuttig zijn voor complexere integralen of wanneer we snel een oplossing nodig hebben.
Het beheersen van trigonometrische integralen zoals ∫ 1/(sin x - a sin x - b) dx vereist oefening en een goed begrip van trigonometrische identiteiten en integratietechnieken. Door deze concepten onder de knie te krijgen, openen we een wereld van mogelijkheden om complexe wiskundige problemen op te lossen en een dieper inzicht te krijgen in de schoonheid en elegantie van de wiskunde.
Maria moeder van god en onze moeder een spirituele reis
Nederland onder water kaart de onthullende waarheid
Auto onderdelen vinden in texas via craigslist de ultieme gids