Ontdek de Magie van Sinus, Cosinus en Tangens!
Stel je voor: je bent op een zonnige dag aan het wandelen en je ziet een prachtige regenboog aan de hemel. Heb je je ooit afgevraagd hoe wetenschappers de hoek van die regenboog berekenen? Of hoe architecten de perfecte helling van een dak bepalen? Dat kan allemaal dankzij de wondere wereld van de trigonometrie, met zijn heldendriehoek: sinus, cosinus en tangens – vaak afgekort als sin, cos en tan.
Sinus, cosinus en tangens zijn als de specerijen in de keuken van de wiskunde. Ze geven ons de tools om de relatie tussen hoeken en zijden in rechthoekige driehoeken te beschrijven. Deze driehoekige genieën zijn onmisbaar in talloze vakgebieden, van natuurkunde en techniek tot muziek en grafisch ontwerp.
De geschiedenis van sin, cos en tan gaat eeuwen terug tot de oude Babyloniërs en Grieken. Zij gebruikten trigonometrie voor astronomie, navigatie en landmeting. Denk aan de sterrenhemel navigeren met alleen de sterren als kompas – dat is de kracht van sin, cos en tan!
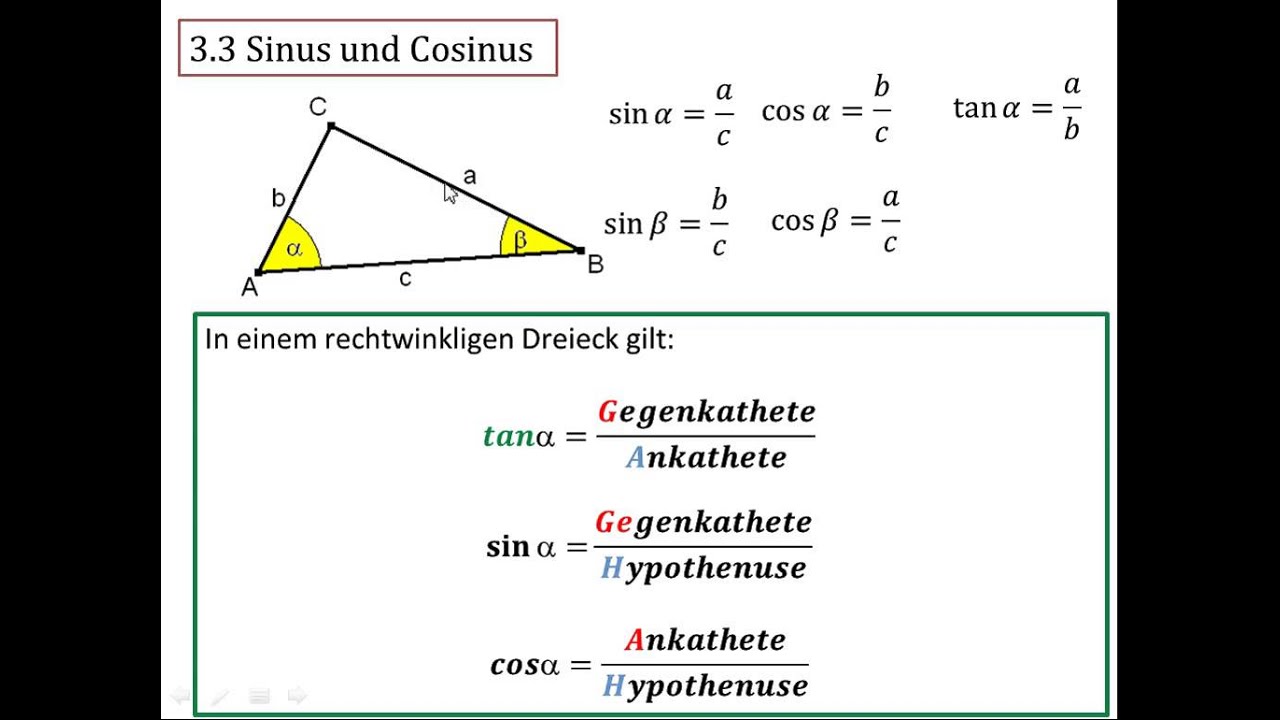
Maar laten we deze wiskundige superhelden eens van dichtbij bekijken. Simpel gezegd, sin, cos en tan zijn verhoudingen van de lengtes van de zijden in een rechthoekige driehoek. De sinus van een hoek is de verhouding tussen de overstaande zijde en de schuine zijde. Cosinus is de verhouding tussen de aanliggende zijde en de schuine zijde, terwijl tangens de verhouding is tussen de overstaande en de aanliggende zijde.
Waarom is dit belangrijk? Nou, met deze verhoudingen kunnen we onbekende zijden of hoeken in een rechthoekige driehoek berekenen. Stel je voor dat je de hoogte van een boom wilt weten. Je kunt de afstand tot de boom meten en de hoek naar de top bepalen. Met de tangens van die hoek en de gemeten afstand kun je de hoogte van de boom berekenen! Handig, toch?
Voordelen van Sinus, Cosinus en Tangens
Sinus, cosinus en tangens bieden talloze voordelen in verschillende toepassingen:
- Navigatie: Van schepen op zee tot vliegtuigen in de lucht, sin, cos en tan helpen bij het bepalen van de juiste koers en positie.
- Bouwkunde: Architecten gebruiken deze functies om de hellingshoek van daken, de lengte van balken en de stabiliteit van constructies te berekenen.
- Computergraphics: Sin, cos en tan spelen een cruciale rol bij het creëren van realistische 3D-beelden en animaties in games en films.
Veelgestelde Vragen over Sin, Cos en Tan
Hier zijn enkele veelgestelde vragen over sinus, cosinus en tangens:
- Wat is het verschil tussen sinus, cosinus en tangens? Sinus is de verhouding tussen overstaande en schuine zijde, cosinus tussen aanliggende en schuine zijde, en tangens tussen overstaande en aanliggende zijde.
- Hoe kan ik sinus, cosinus en tangens onthouden? Een ezelsbruggetje is "SOS CAS TOA": Sinus = Overstaande / Schuine, Cosinus = Aanliggende / Schuine, Tangens = Overstaande / Aanliggende.
- Waar kan ik meer leren over trigonometrie? Online bronnen zoals Khan Academy en wiskundeboeken bieden uitgebreide informatie over dit onderwerp.
Conclusie
Sinus, cosinus en tangens vormen de basis van de trigonometrie en spelen een cruciale rol in ons dagelijks leven, van de technologie die we gebruiken tot de gebouwen waarin we wonen. Hoewel ze in het begin misschien complex lijken, onthoud dan dat deze wiskundige functies hulpmiddelen zijn die ons helpen de wereld om ons heen te begrijpen en te vormen. Of je nu een student, professional of gewoon nieuwsgierig bent, de wereld van sin, cos en tan is er een vol fascinerende ontdekkingen!
De fascinerende wereld van de tweede afgeleide van lnx
De tijdloze magie van ik blijf bij jou gunther neefs
Overzicht van al je waarden duidelijkheid en richting