Meer dan & Minder dan Tekens: Onmisbaar in Wiskunde & Programmeren
Wat is groter, 5 of 10? Een simpele vraag met een even simpel antwoord. Maar hoe drukken we die relatie mathematisch uit? Daar komen de 'meer dan' en 'minder dan' tekens (> en <) in beeld. Deze ogenschijnlijk eenvoudige symbolen spelen een cruciale rol in de wiskunde, programmeren en zelfs in ons dagelijks leven, van het vergelijken van prijzen tot het analyseren van data.
De 'meer dan' en 'minder dan' tekens, ook wel bekend als ongelijkheidstekens, vormen de basis van vergelijkingen en rangschikkingen. Ze helpen ons de relatie tussen twee waarden te begrijpen en te definiëren. Stel je voor een wereld zonder deze symbolen. Het vergelijken van getallen zou een stuk omslachtiger zijn.
In de wereld van data-analyse en programmeren zijn deze tekens onmisbaar. Ze vormen de bouwstenen van complexe algoritmes en logische operaties. Denk aan zoekopdrachten, filters en voorwaardelijke statements. Zonder de 'meer dan' en 'minder dan' tekens zouden deze functies simpelweg niet bestaan.
Dit artikel duikt diep in de wereld van de 'meer dan' en 'minder dan' tekens. We verkennen hun oorsprong, betekenis en toepassingen. Van eenvoudige wiskundige vergelijkingen tot complexe programmeerlogica, we laten zien hoe deze symbolen ons helpen de wereld om ons heen te begrijpen en te manipuleren.
Bereid je voor op een fascinerende reis door de wereld van > en <! We zullen zien hoe deze kleine tekens een grote impact hebben op ons begrip van getallen, data en de digitale wereld.
De geschiedenis van deze symbolen gaat terug tot de 17e eeuw, met Thomas Harriot die ze introduceerde. Hun belang is sindsdien alleen maar toegenomen, vooral met de opkomst van computerwetenschappen.
Definities:
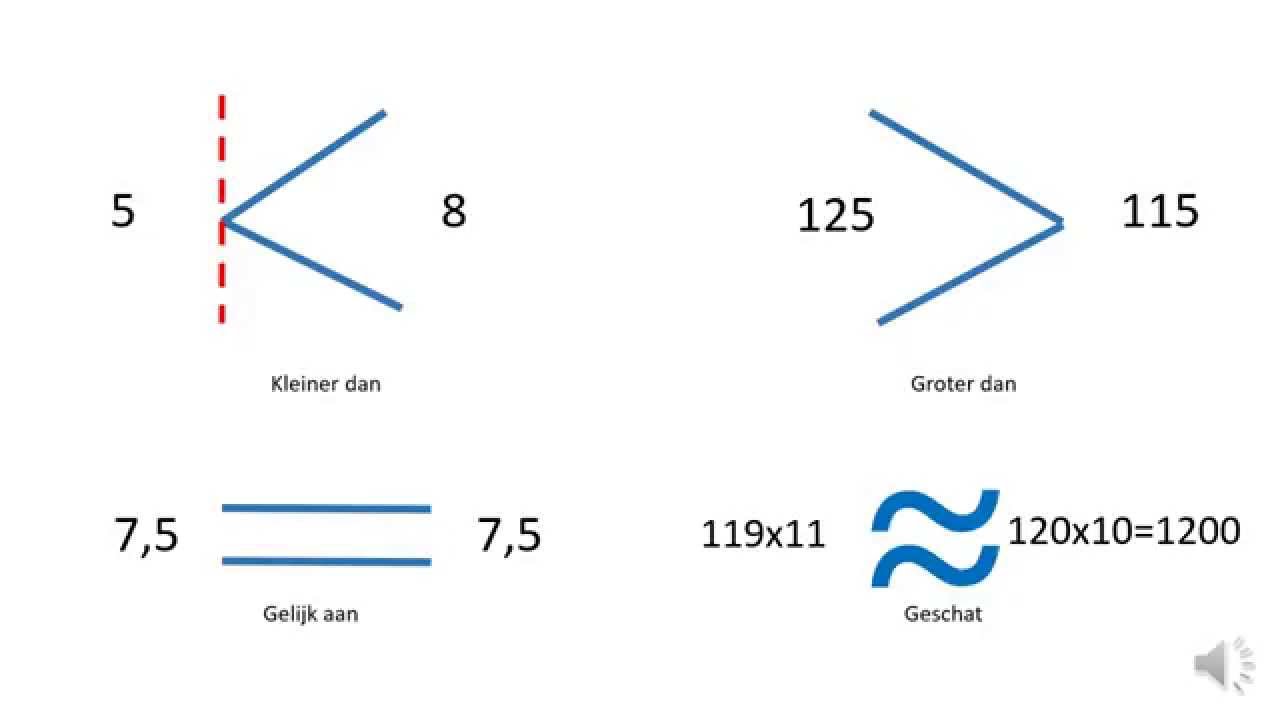
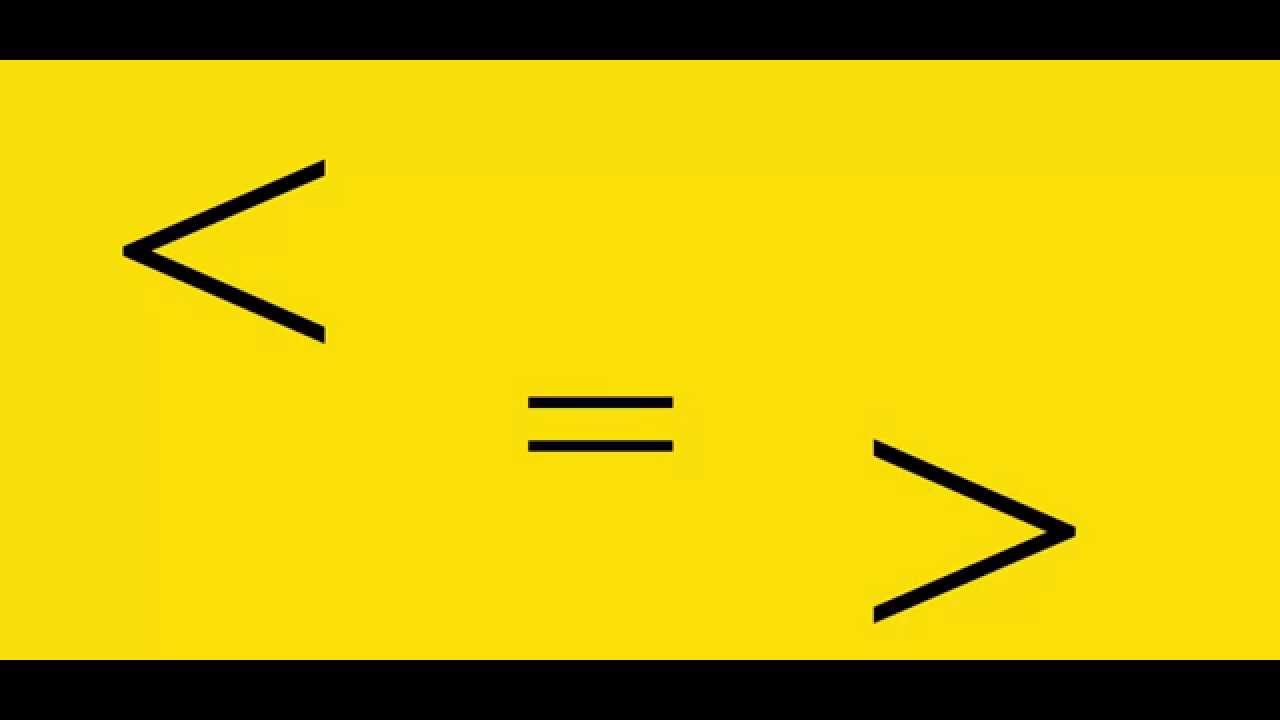
> (groter dan): Geeft aan dat de waarde links van het teken groter is dan de waarde rechts. Bijvoorbeeld: 10 > 5.
< (kleiner dan): Geeft aan dat de waarde links van het teken kleiner is dan de waarde rechts. Bijvoorbeeld: 5 < 10.
Voordelen:
1. Duidelijkheid: Ze bieden een universeel begrepen manier om waarden te vergelijken.
2. Efficiëntie: Ze vereenvoudigen complexe wiskundige en programmeerconcepten.
3. Essentieel voor logica: Vormen de basis van voorwaardelijke statements in programmeren.
Voor- en Nadelen van Meer dan en Minder dan Tekens
| Voordelen | Nadelen |
|---|---|
| Universeel begrip | Verwarring met andere symbolen (bijv. chevrons) |
| Eenvoudige implementatie | Beperkt tot numerieke en sommige string vergelijkingen |
Beste Praktijken:
1. Gebruik de juiste teken voor de gewenste vergelijking.
2. Zorg voor consistente spacing rondom de tekens.
3. Combineer met = voor 'groter dan of gelijk aan' (≥) en 'kleiner dan of gelijk aan' (≤).
4. Test code grondig om onbedoelde fouten te voorkomen.
5. Documenteer de logica achter vergelijkingen in code.
Voorbeelden:
1. 15 > 10 (Vijftien is groter dan tien)
2. 7 < 12 (Zeven is kleiner dan twaalf)
3. x > 0 (x is groter dan nul)
4. y < 100 (y is kleiner dan honderd)
5. temperatuur > 25 (Temperatuur is groter dan 25 graden)
Veelgestelde Vragen:
1. Wat is het verschil tussen > en <? (> betekent groter dan, < betekent kleiner dan)
2. Hoe gebruik ik deze tekens in programmeren? (In voorwaardelijke statements, loops, etc.)
3. Wat is ≥? (Groter dan of gelijk aan)
4. Wat is ≤? (Kleiner dan of gelijk aan)
5. Kan ik deze tekens gebruiken met tekst? (Ja, voor alfabetische volgorde)
6. Wat gebeurt er als ik de tekens verkeerd gebruik? (Onverwachte resultaten in code of onjuiste wiskundige beweringen)
7. Waar kan ik meer informatie vinden? (Wiskundeboeken, programmeer documentatie)
8. Hoe onthoud ik welk teken wat betekent? (De punt van het teken wijst naar het kleinere getal.)
Tips & Trucs: Denk aan de "krokodilbek" die altijd het grootste getal "opeet". Dit kan helpen bij het onthouden van de richting van de tekens.
De 'meer dan' en 'minder dan' tekens zijn onmisbare instrumenten in de wiskunde en programmeren. Ze bieden een duidelijke, efficiënte en universeel begrepen manier om waarden te vergelijken en relaties tussen getallen te definiëren. Van eenvoudige rekenkundige vergelijkingen tot complexe algoritmes, deze symbolen spelen een cruciale rol in ons begrip van data en de digitale wereld. Het correct gebruiken van deze tekens is essentieel voor accurate berekeningen, effectieve programmering en een helder begrip van wiskundige concepten. Door de tips en voorbeelden in dit artikel te volgen, kunt u uw begrip van deze fundamentele symbolen verdiepen en hun krachtige toepassingen in de praktijk brengen. Investeer tijd in het beheersen van deze ogenschijnlijk eenvoudige, maar essentiële concepten, en u zult de vruchten ervan plukken in uw wiskundige en programmeervaardigheden. Neem de tijd om te oefenen met verschillende voorbeelden en ontdek de veelzijdigheid van deze krachtige symbolen.
Gevolgen van roken leer de risicos
Bananenpower ontdek de magie van deze gele fruitbom
Ontdek de magie van muziek voor verschillende instrumenten