De Tangens: Ontdek de Kracht van Trigonometrie
Stel je voor: je staat aan de voet van een majestueuze berg, de top gehuld in nevelen. Je wilt de hoogte van deze reusachtige rotsformatie bepalen, maar de steile wanden maken directe metingen onmogelijk. Hier komt de kracht van trigonometrie, en meer specifiek de tangens, om de hoek kijken.
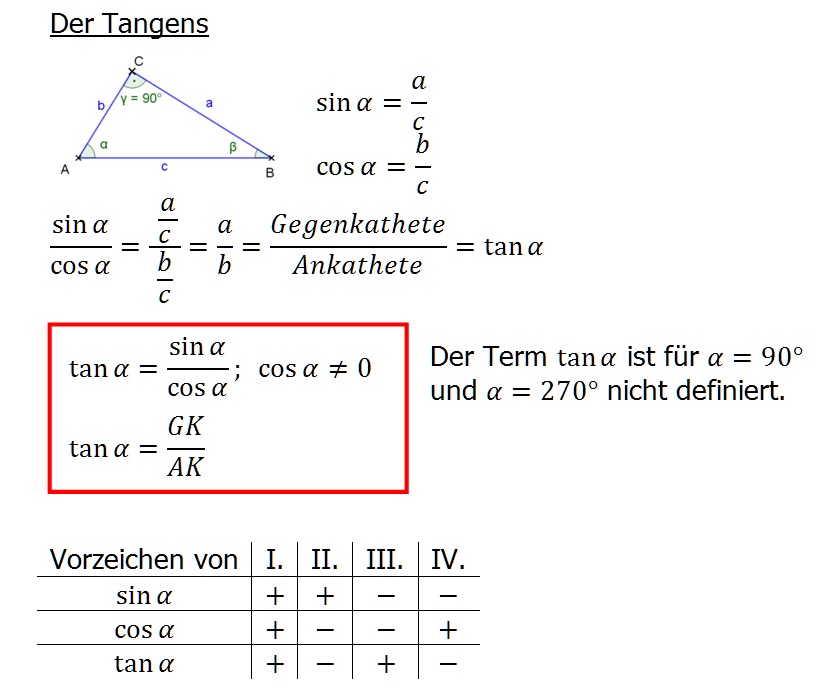
De term "tangens" is afkomstig van het Latijnse woord "tangere," wat "aanraken" betekent. In de wiskunde raakt de tangens echter niet alleen aan de oppervlakte; het duikt diep in de relatie tussen hoeken en zijden in rechthoekige driehoeken. De tangens van een hoek in een rechthoekige driehoek wordt gedefinieerd als de verhouding tussen de lengte van de overstaande zijde en de lengte van de aanliggende zijde. Deze ogenschijnlijk eenvoudige verhouding opent de deur naar een breed scala aan toepassingen in verschillende disciplines, van landmeting en navigatie tot natuurkunde en engineering.
De geschiedenis van de tangens gaat terug tot de oude beschavingen van Egypte en Mesopotamië, waar astronomen en landmeters trigonometrische concepten gebruikten om afstanden tot hemellichamen te berekenen en land te verdelen. De Griekse astronoom Hipparchus van Nicea, die leefde in de 2e eeuw voor Christus, wordt beschouwd als de vader van de trigonometrie en zijn werk aan trigonometrische tabellen legde de basis voor verdere ontwikkelingen in het veld.
Het belang van de tangens ligt in zijn vermogen om onbekende afstanden en hoeken te berekenen met behulp van bekende waarden. Dit maakt het een onmisbaar hulpmiddel in de landmeetkunde, waar het wordt gebruikt om de hoogte van gebouwen, bomen en andere objecten te bepalen, evenals de afstand over rivieren en kloven. In de navigatie helpt de tangens bij het bepalen van de koers en positie van schepen en vliegtuigen, vooral in situaties waarin GPS-systemen niet beschikbaar zijn.
Naast praktische toepassingen speelt de tangens ook een cruciale rol in de natuurkunde, vooral in de mechanica en optica. In de mechanica wordt de tangens gebruikt om de krachten die op objecten inwerken te analyseren, bijvoorbeeld bij het bestuderen van de beweging van projectielen of de stabiliteit van constructies. In de optica helpt de tangens bij het begrijpen van de breking van licht, wat essentieel is voor het ontwerpen van lenzen en andere optische instrumenten.
Voordelen van de Tangens
De tangens biedt tal van voordelen in verschillende toepassingen:
- Bepalen van onbekende afstanden: Met behulp van de tangens en een bekende hoek en zijde in een rechthoekige driehoek kunnen we de lengte van de andere zijden berekenen. Dit is met name handig in de landmeetkunde en navigatie.
- Analyseren van krachten en beweging: In de natuurkunde helpt de tangens bij het ontbinden van krachten in componenten en het bestuderen van de beweging van objecten onder invloed van deze krachten.
- Ontwerpen van optische instrumenten: De tangens is essentieel voor het begrijpen van de breking van licht en het ontwerpen van lenzen, prisma's en andere optische componenten.
De Tangens in de Praktijk
Laten we eens kijken naar enkele concrete voorbeelden van hoe de tangens wordt gebruikt:
- De hoogte van een boom bepalen: Meet de afstand van de boom tot een punt op de grond waar je de top van de boom kunt zien. Meet vervolgens de hoek tussen je kijklijn naar de top van de boom en de horizontaal. Met behulp van de tangens van deze hoek en de gemeten afstand kun je de hoogte van de boom berekenen.
- De breedte van een rivier bepalen: Kies een punt aan de overkant van de rivier. Loop langs de oever totdat je een punt vindt waar de hoek tussen je kijklijn naar het punt aan de overkant en de oever 45 graden is. De afstand die je langs de oever hebt gelopen, is gelijk aan de breedte van de rivier.
- De helling van een weg berekenen: De tangens van de hellingshoek van een weg is gelijk aan de verhouding tussen het hoogteverschil en de horizontale afstand over een bepaald deel van de weg. Dit geeft een indicatie van hoe steil de weg is.
Veelgestelde Vragen over de Tangens
Hier zijn enkele veelgestelde vragen over de tangens:
- Wat is het verschil tussen sinus, cosinus en tangens? Sinus, cosinus en tangens zijn trigonometrische functies die de verhoudingen tussen de zijden en hoeken van een rechthoekige driehoek beschrijven. De sinus van een hoek is de verhouding tussen de overstaande zijde en de schuine zijde. De cosinus is de verhouding tussen de aanliggende zijde en de schuine zijde. De tangens is de verhouding tussen de overstaande zijde en de aanliggende zijde.
- Wat is de eenheid van de tangens? De tangens is een dimensieloze grootheid, wat betekent dat het geen eenheid heeft. Het is een zuiver getal dat een verhouding aangeeft.
- Kan de tangens groter zijn dan 1? Ja, de tangens kan groter zijn dan 1. Dit gebeurt wanneer de overstaande zijde van een rechthoekige driehoek langer is dan de aanliggende zijde, wat betekent dat de hoek groter is dan 45 graden.
Conclusie
De tangens is een fundamenteel concept in de trigonometrie met een breed scala aan toepassingen in verschillende disciplines. Van het bepalen van de hoogte van een berg tot het analyseren van krachten in de natuurkunde, de tangens stelt ons in staat om de wereld om ons heen te meten, te begrijpen en te manipuleren. Door de kracht van de tangens te benutten, kunnen we complexe problemen oplossen, innovatieve oplossingen ontwikkelen en onze kennis van het universum vergroten. Dus de volgende keer dat je geconfronteerd wordt met een uitdaging waarbij hoeken en afstanden een rol spelen, denk dan aan de tangens en laat deze krachtige trigonometrische functie je gids zijn.
Volvo truck dealerships openingstijden bij jou in de buurt
Border collie duitse herder mix temperament de ultieme gids
Gedichten met een lach en een traan emoties in dichtvorm