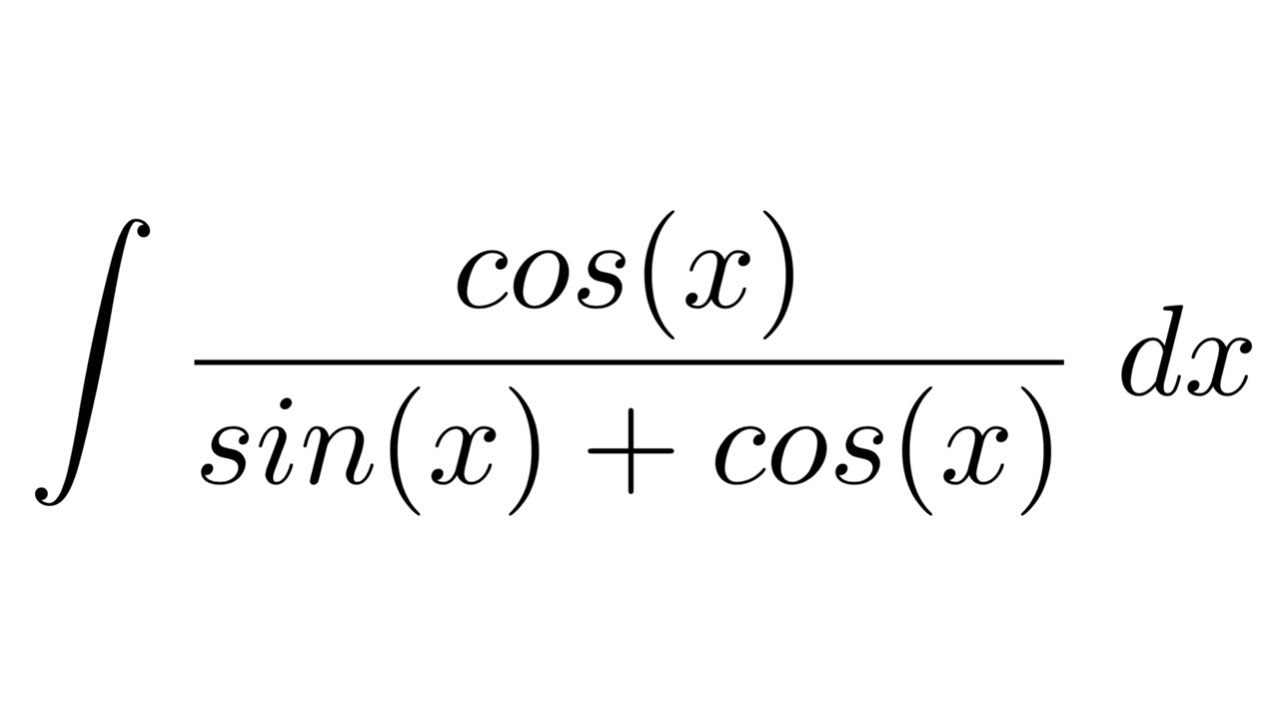De Integraal van cos(x)sin(x): Ontdek de Schoonheid van Calculus
Stel je voor: de glooiende lijnen van een grafiek, dansend op het ritme van trigonometrische functies. In het hart van deze dans vinden we de integraal van cos(x)sin(x), een elegante formule die de schoonheid van calculus onthult. Deze integraal, meer dan alleen een wiskundige berekening, opent een wereld van toepassingen in de fysica, engineering en daarbuiten.
De integraal van cos(x)sin(x) is als een kameleon, die zich transformeert afhankelijk van de context. Soms verschijnt het in de berekening van oppervlakten en volumes, terwijl het op andere momenten de sleutel is tot het begrijpen van complexe trillingen en golven.
Maar laten we, voordat we ons verdiepen in de details, een stap terug doen. Wat is een integraal precies? Simpel gezegd, een integraal is een manier om de oppervlakte onder een kromme te berekenen. In het geval van cos(x)sin(x), berekenen we de oppervlakte onder de golvende lijn die deze functie beschrijft.
De geschiedenis van integralen gaat terug tot de oude Grieken, maar het waren Isaac Newton en Gottfried Leibniz die de basis legden voor de moderne calculus. Zij ontwikkelden de fundamentele stelling van de calculus, die ons in staat stelt integralen te berekenen door gebruik te maken van afgeleiden.
De integraal van cos(x)sin(x) is een prachtig voorbeeld van hoe calculus ons kan helpen complexe problemen op te lossen. Het is een hulpmiddel om de wereld om ons heen beter te begrijpen, van de kleinste trillingen tot de beweging van planeten.
Voordelen en Nadelen van het Gebruik van integral cos x sin x
| Voordelen | Nadelen |
|---|---|
| Toepasbaar in diverse disciplines | Vereist kennis van calculus |
| Helpt complexe problemen oplossen | Kan computationeel intensief zijn |
Veelgestelde Vragen
1. Wat is de integraal van cos(x)sin(x)?
De integraal van cos(x)sin(x) is -(1/2)cos^2(x) + C, waarbij C een integratieconstante is.
2. Hoe los ik de integraal van cos(x)sin(x) op?
De integraal kan worden opgelost met behulp van substitutie. Stel u = cos(x), dan is du = -sin(x)dx. Substitueer deze waarden in de integraal en los op.
3. Wat zijn enkele toepassingen van integral cos x sin x?
De integraal heeft toepassingen in de fysica (bijvoorbeeld bij het berekenen van arbeid en energie), engineering (bijvoorbeeld bij signaalverwerking) en andere disciplines.
Conclusie
De integraal van cos(x)sin(x), hoewel ogenschijnlijk een eenvoudige formule, onthult de elegantie en kracht van calculus. Het is een venster naar een wereld van toepassingen, van het begrijpen van de fysieke wereld tot het oplossen van complexe technische problemen. Door de principes van calculus te begrijpen, kunnen we de schoonheid en complexiteit van de wereld om ons heen beter waarderen.
Bull terrier puppies te koop in north carolina
Vijfletterwoorden beginnend met p en eindigend op a ontdek de magie
Hoe snel is een renpaard ontdek de fascinerende snelheid
