Rahsia Mengira Panjang Sisi Segitiga Dengan Mudah
Pernahkah anda meneliti bentuk geometri dan tertanya-tanya bagaimana setiap sisi dan sudutnya diukur? Dunia geometri memang penuh dengan misteri, tetapi dengan sedikit ilmu, kita dapat menyingkap rahsianya. Salah satu misteri yang sering membingungkan adalah cara mengira panjang sisi segitiga. Jangan risau, artikel ini akan membimbing anda untuk memahami dan menguasai teknik-teknik mengira panjang sisi segitiga dengan mudah dan pantas.
Sejak zaman dahulu lagi, manusia telah menggunakan prinsip geometri dalam pelbagai bidang, dari pembinaan piramid megah di Mesir hingga ke reka bentuk bangunan pencakar langit moden. Segitiga, sebagai salah satu bentuk geometri asas, memainkan peranan penting dalam pelbagai aplikasi ini. Kemampuan untuk mengira panjang sisi segitiga menjadi kunci utama dalam memastikan kestabilan struktur, ketepatan pengukuran, dan kejayaan pelbagai projek kejuruteraan.
Masalah utama yang sering dihadapi dalam mengira panjang sisi segitiga adalah kurangnya pemahaman tentang konsep dan formula yang terlibat. Ramai yang menganggap geometri sebagai subjek yang rumit dan abstrak. Namun, sebenarnya, dengan pendekatan yang betul, sesiapa sahaja boleh menguasai konsep ini. Artikel ini akan membimbing anda langkah demi langkah melalui pelbagai kaedah mengira panjang sisi segitiga, dari formula asas seperti Teorem Pythagoras hingga teknik trigonometri yang lebih kompleks.
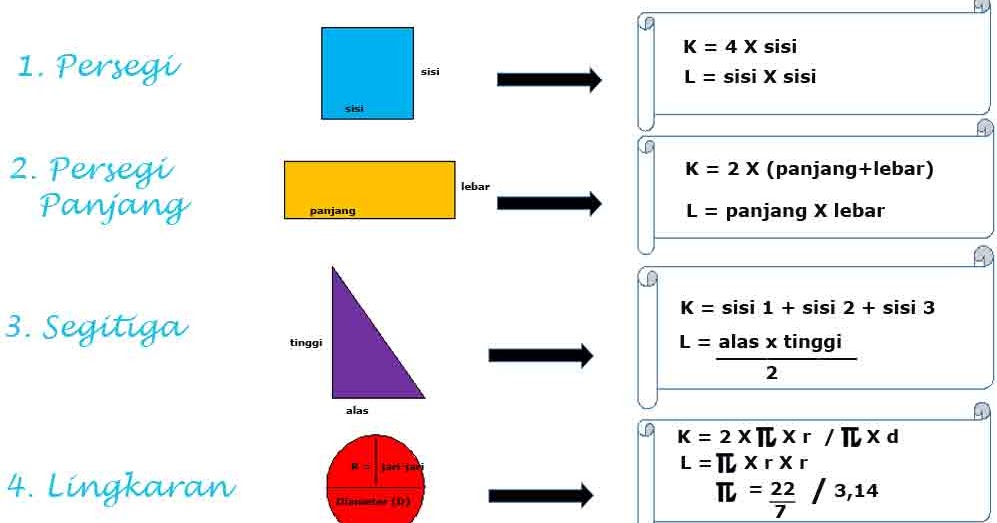
Sebelum kita menyelami lebih mendalam, mari kita fahami terlebih dahulu jenis-jenis segitiga. Segitiga boleh diklasifikasikan berdasarkan panjang sisi dan sudutnya. Berdasarkan panjang sisi, terdapat tiga jenis segitiga: segitiga sama sisi (semua sisi sama panjang), segitiga sama kaki (dua sisi sama panjang), dan segitiga tak sama sisi (semua sisi berbeza panjang). Berdasarkan sudutnya, terdapat segitiga bersudut tegak (mempunyai satu sudut tepat 90 darjah), segitiga bersudut tirus (semua sudut kurang dari 90 darjah), dan segitiga bersudut cakah (mempunyai satu sudut lebih dari 90 darjah).
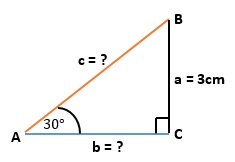
Memahami jenis-jenis segitiga ini penting kerana ia mempengaruhi kaedah yang digunakan untuk mengira panjang sisinya. Contohnya, untuk segitiga bersudut tegak, kita boleh menggunakan Teorem Pythagoras yang terkenal, iaitu a² + b² = c², di mana a dan b adalah panjang sisi tegak dan c adalah panjang sisi miring (hipotenus). Bagi segitiga lain, kita mungkin perlu menggunakan Hukum Sinus atau Hukum Kosinus, yang akan kita bincangkan dengan lebih lanjut kemudian.
Kelebihan dan Kekurangan Mengira Panjang Sisi Segitiga
| Kelebihan | Kekurangan |
|---|---|
| Dapat diaplikasikan dalam pelbagai bidang seperti kejuruteraan, seni bina, dan navigasi | Memerlukan pemahaman tentang konsep dan formula geometri |
| Membantu menyelesaikan masalah dunia sebenar yang melibatkan bentuk dan ukuran | Ketepatan pengiraan bergantung pada ketepatan pengukuran awal |
Lima Amalan Terbaik untuk Mengira Panjang Sisi Segitiga
Berikut adalah beberapa amalan terbaik yang boleh membantu anda mengira panjang sisi segitiga dengan lebih tepat dan efisien:
- Kenal pasti jenis segitiga: Langkah pertama dan paling penting adalah mengenal pasti jenis segitiga yang anda hadapi. Ini akan membantu anda memilih formula atau kaedah yang sesuai untuk digunakan.
- Lukis gambar rajah: Melukis gambar rajah segitiga dan menandakan semua maklumat yang diberikan dapat membantu anda memvisualisasikan masalah dengan lebih jelas. Ini juga memudahkan anda untuk mengenal pasti sisi dan sudut yang perlu dikira.
- Pilih formula yang betul: Pastikan anda memilih formula yang sesuai dengan jenis segitiga dan maklumat yang diberikan. Jangan teragak-agak untuk merujuk kembali kepada buku teks atau sumber rujukan lain jika perlu.
- Gunakan kalkulator: Untuk pengiraan yang melibatkan nombor perpuluhan atau sudut, menggunakan kalkulator saintifik akan memastikan ketepatan hasil anda.
- Semak jawapan anda: Selepas membuat pengiraan, luangkan masa untuk menyemak semula jawapan anda. Pastikan jawapan anda munasabah dan sepadan dengan konteks masalah.
Soalan Lazim Mengenai Mengira Panjang Sisi Segitiga
Berikut adalah beberapa soalan lazim mengenai mengira panjang sisi segitiga:
- Apakah Teorem Pythagoras?
Teorem Pythagoras menyatakan bahawa dalam segitiga bersudut tegak, kuasadua panjang sisi miring (hipotenus) sama dengan jumlah kuasadua panjang dua sisi tegak. Ia boleh ditulis sebagai a² + b² = c², di mana a dan b adalah panjang sisi tegak dan c adalah panjang sisi miring. - Bagaimana cara mengira panjang sisi miring segitiga bersudut tegak?
Untuk mengira panjang sisi miring segitiga bersudut tegak, gunakan Teorem Pythagoras: c = √(a² + b²), di mana a dan b adalah panjang sisi tegak. - Bagaimana cara mengira panjang sisi tegak segitiga bersudut tegak?
Untuk mengira panjang sisi tegak segitiga bersudut tegak, gunakan Teorem Pythagoras: a = √(c² - b²) atau b = √(c² - a²), di mana c adalah panjang sisi miring dan a atau b adalah panjang sisi tegak yang lain.
Menguasai teknik mengira panjang sisi segitiga membuka pintu kepada pelbagai peluang dalam bidang STEM dan seterusnya. Sama ada anda seorang pelajar, profesional, atau sekadar ingin mengasah kemahiran matematik anda, meluangkan masa untuk memahami konsep ini pasti akan memberi manfaat yang besar. Ingatlah untuk terus berlatih, jangan takut untuk meminta bantuan, dan yang paling penting, nikmati proses pembelajaran!
Membuktikan dedikasi memahami surat pengesahan dalam perkhidmatan
Menghayati eratnya silaturahim jemputan ke majlis tahlil
Mendidik hati menanam benih cinta al quran sejak kecil dengan surah al qadr
![Cara Mudah Membuat Flowchart Yang Baik dan Benar [LENGKAP]](https://i2.wp.com/sharingconten.com/wp-content/uploads/2020/01/Flowchart-Menghitung-Luas-Segitiga.jpg)
