Mengenal Fungsi dalam Matematik: Rahsia Hubungan Angka yang Menarik
Pernahkah anda terfikir bagaimana suhu badan kita berubah sepanjang hari atau bagaimana harga barang di pasaran dipengaruhi oleh permintaan? Jawapannya terletak pada konsep 'fungsi' dalam matematik. Fungsi, ibarat mesin ajaib yang menghubungkan satu set input kepada satu set output mengikut peraturan tertentu. Konsep ini menjadi nadi dalam pelbagai bidang, dari sains dan teknologi hinggalah ekonomi dan kehidupan seharian kita.
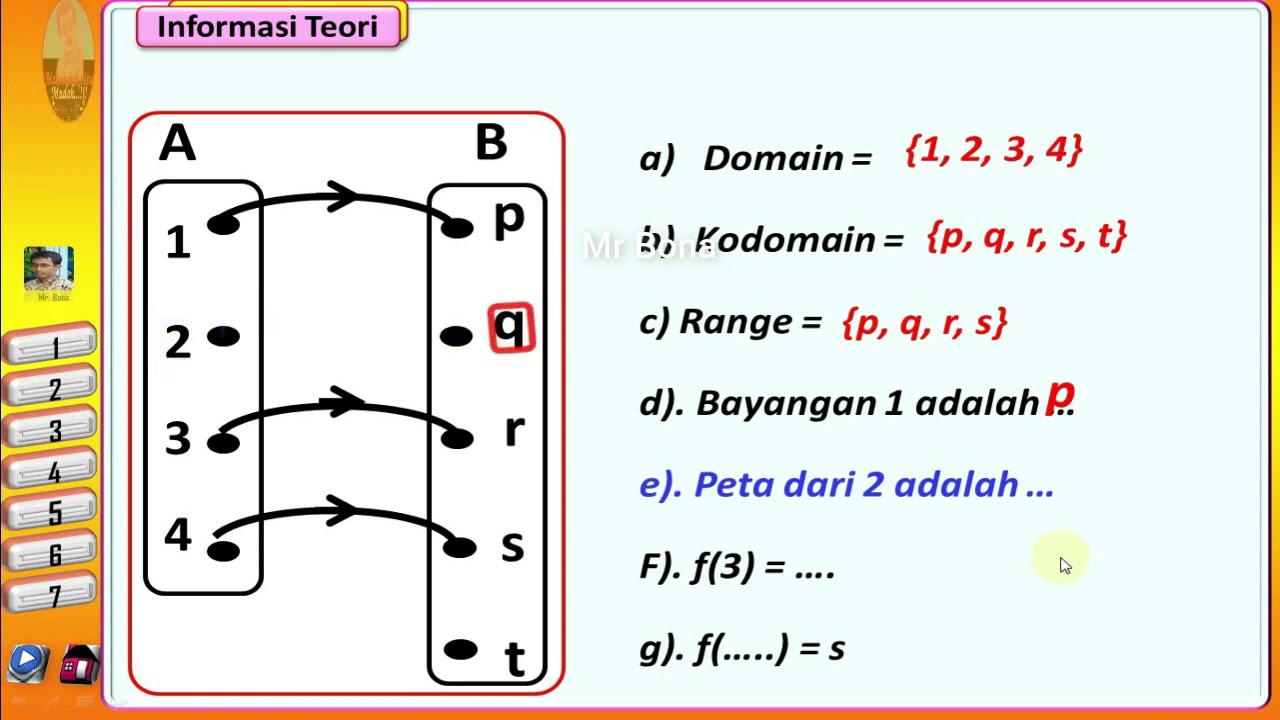
Bayangkan fungsi seperti mesin pembuat jus. Kita masukkan buah-buahan (input) ke dalam mesin, dan ia menghasilkan jus (output) mengikut jenis buah yang dimasukkan. Begitu juga dengan fungsi dalam matematik. Ia mengambil nilai input (dipanggil domain) dan menghasilkan nilai output (dipanggil julat) berdasarkan peraturan yang telah ditetapkan.
Sejarah fungsi dalam matematik bermula sejak zaman Yunani kuno, di mana ahli falsafah dan matematik seperti Pythagoras dan Euclid mengkaji hubungan antara nombor dan bentuk. Konsep fungsi secara formal diperkenalkan pada abad ke-17 oleh Gottfried Wilhelm Leibniz, seorang ahli matematik dan falsafah Jerman. Beliau menggunakan istilah 'fungsi' untuk menggambarkan kuantiti yang bergantung pada kuantiti lain.
Fungsi memainkan peranan penting dalam pelbagai cabang matematik, termasuk algebra, kalkulus, dan statistik. Ia membantu kita memodelkan dan menganalisis fenomena dunia sebenar, meramalkan trend masa depan, dan menyelesaikan masalah kompleks. Sebagai contoh, fungsi digunakan untuk memodelkan pertumbuhan populasi, pergerakan objek, dan juga penyebaran penyakit.
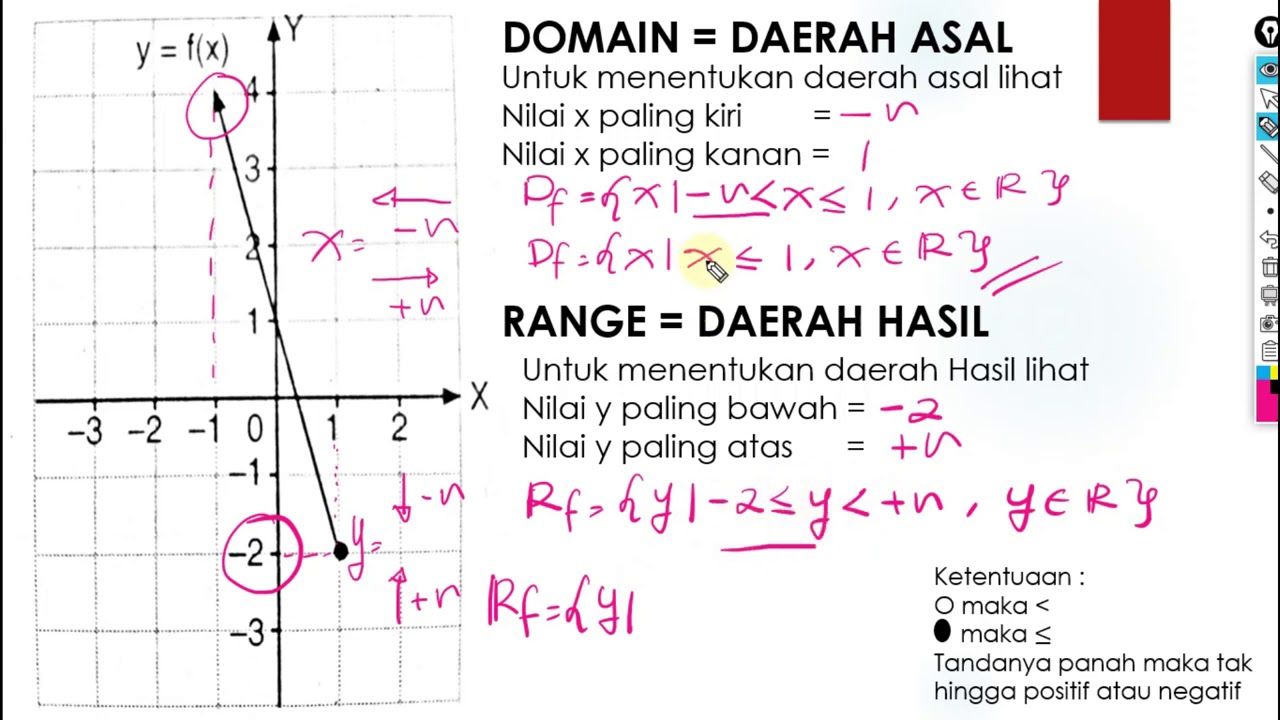
Fungsi boleh diwakili dalam pelbagai cara, termasuk persamaan matematik, graf, jadual, dan gambar rajah. Setiap perwakilan mempunyai kelebihan dan kekurangan tersendiri. Persamaan matematik memberikan gambaran yang tepat tentang hubungan antara input dan output, manakala graf membolehkan kita memvisualisasikan fungsi dan mengenal pasti ciri-cirinya dengan mudah.
Salah satu jenis fungsi yang paling asas ialah fungsi linear. Fungsi ini mempunyai graf berbentuk garis lurus dan diwakili oleh persamaan y = mx + c, di mana m ialah kecerunan dan c ialah pintasan-y. Fungsi linear digunakan secara meluas dalam kehidupan seharian, contohnya untuk mengira kos perjalanan teksi berdasarkan jarak yang dilalui.
Selain fungsi linear, terdapat juga pelbagai jenis fungsi lain, seperti fungsi kuadratik, fungsi eksponen, dan fungsi trigonometri. Setiap jenis fungsi mempunyai ciri-ciri dan aplikasi tersendiri. Sebagai contoh, fungsi kuadratik digunakan untuk memodelkan trajektori objek yang dilambung, manakala fungsi eksponen digunakan untuk memodelkan pertumbuhan populasi bakteria.
Memahami konsep fungsi adalah sangat penting untuk pelajar matematik pada semua peringkat. Ia membuka pintu kepada pelbagai topik matematik yang lebih kompleks dan menyediakan asas yang kukuh untuk meneroka bidang STEM (Sains, Teknologi, Kejuruteraan, dan Matematik) yang lebih luas.
Kelebihan dan Kekurangan Fungsi dalam Matematik
Seperti konsep matematik yang lain, fungsi juga mempunyai kelebihan dan kekurangannya tersendiri.
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pemahaman tentang hubungan antara pembolehubah. | Boleh menjadi rumit untuk memahami fungsi yang kompleks. |
| Membolehkan kita memodelkan dan menyelesaikan masalah dunia sebenar. | Terdapat beberapa situasi di mana fungsi tidak dapat digunakan. |
| Mempunyai aplikasi yang luas dalam pelbagai bidang. | Memerlukan pemahaman yang kukuh tentang konsep matematik asas. |
Walaupun fungsi mempunyai beberapa kekurangan, kelebihannya jauh lebih banyak. Dengan memahami konsep fungsi, kita dapat lebih menghargai keindahan dan kekuatan matematik dalam menerangkan dunia di sekeliling kita.
Srikandi tanah jawa menelusuri jejak pahlawan perempuan indonesia
Artikel bermain sambil belajar
Wakil ketua mpr ri siapakah mereka dan apa yang mereka lakukan