Kuasai Rumus Segi Empat Selari: Aplikasi Praktikal & Contoh
Pernahkah anda terfikir bagaimana arkitek mengira ruang lantai sesebuah bangunan atau bagaimana jurutera merancang reka bentuk jambatan yang kukuh? Jawapannya terletak pada pemahaman tentang bentuk geometri dan rumus yang mengawalnya. Salah satu bentuk yang paling asas dan penting ialah segi empat selari, dan rumusnya memainkan peranan penting dalam pelbagai bidang, daripada seni bina hinggalah kejuruteraan.
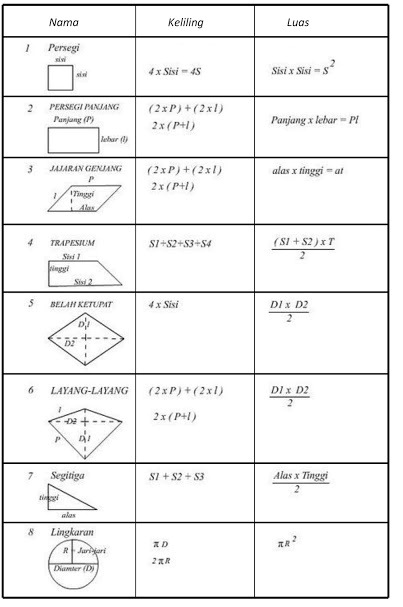
Walaupun kelihatan mudah, rumus segi empat selari – Luas = Tapak x Tinggi – mempunyai aplikasi yang luas. Ia bukan sekadar formula matematik tetapi kunci kepada reka bentuk, pembinaan dan pemahaman dunia fizikal kita.
Sejarah rumus segi empat selari boleh ditarik balik kepada tamadun awal seperti Mesopotamia dan Mesir. Mereka menggunakan konsep geometri untuk pengukuran tanah, pembinaan dan astronomi. Sumbangan mereka meletakkan asas bagi matematik Yunani, di mana Euclid memformalkan sifat-sifat segi empat selari dalam karyanya "Elements."
Rumus segi empat selari mempunyai kepentingan dalam pelbagai bidang. Dalam seni bina, ia digunakan untuk mengira luas lantai, dinding dan bumbung. Jurutera menggunakannya untuk mereka bentuk jambatan, jalan raya dan struktur lain. Pereka grafik menggunakannya untuk mencipta susun atur dan grafik yang seimbang. Malah dalam kehidupan seharian, kita menggunakan rumus ini secara tidak langsung, contohnya, apabila memotong sehelai kertas kepada saiz tertentu.
Memahami rumus segi empat selari memberi beberapa manfaat:
- Pengiraan Luas: Manfaat paling jelas ialah keupayaan untuk mengira luas segi empat selari, yang penting dalam pelbagai aplikasi praktikal seperti menentukan jumlah cat yang diperlukan untuk dinding atau jumlah jubin yang diperlukan untuk lantai.
- Penyelesaian Masalah: Rumus ini berfungsi sebagai alat penyelesaian masalah dalam pelbagai bidang. Contohnya, dalam fizik, ia boleh digunakan untuk mengira kerja yang dilakukan oleh daya yang bertindak pada objek.
- Pemikiran Spatial: Mempelajari tentang segi empat selari dan rumusnya meningkatkan pemikiran spatial, membantu kita membayangkan dan memanipulasi bentuk dalam minda kita, kemahiran yang berharga dalam bidang seperti seni bina, kejuruteraan dan reka bentuk.
Walaupun rumus segi empat selari agak mudah, terdapat beberapa kesilapan biasa yang boleh berlaku:
Kekurangan Rumus Segi Empat Selari
| Kekurangan | Penjelasan |
|---|---|
| Kekeliruan dengan Tinggi dan Lebar | Salah satu kesilapan biasa ialah mengelirukan tinggi dengan lebar. Tinggi segi empat selari sentiasa berserenjang dengan tapak. |
| Penggunaan Unit yang Tidak Konsisten | Adalah penting untuk memastikan bahawa unit yang digunakan untuk tapak dan tinggi adalah sama. |
Untuk memastikan anda menggunakan rumus dengan betul, berikut adalah beberapa amalan terbaik:
- Kenal pasti tapak dan tinggi dengan jelas.
- Pastikan tapak dan tinggi adalah berserenjang.
- Gunakan unit yang sama untuk tapak dan tinggi.
- Semak semula pengiraan anda.
- Amalkan menggunakan rumus dalam pelbagai situasi.
Berikut adalah beberapa contoh penggunaan rumus segi empat selari dalam situasi dunia sebenar:
- Seorang arkitek menggunakan rumus untuk mengira luas lantai sebuah bilik segi empat tepat untuk menentukan jumlah jubin yang diperlukan.
- Seorang jurutera menggunakan rumus untuk mengira luas keratan rentas rasuk untuk menentukan kekuatannya.
- Seorang petani menggunakan rumus untuk mengira luas ladangnya untuk menentukan jumlah tanaman yang boleh ditanamnya.
- Seorang artis menggunakan rumus untuk mengira luas kanvas yang diperlukan untuk lukisan.
- Seorang tukang kayu menggunakan rumus untuk mengira luas sehelai kayu yang diperlukan untuk projek.
Memahami rumus segi empat selari adalah penting dalam pelbagai bidang. Ia adalah konsep asas yang mempunyai aplikasi praktikal yang tidak terkira banyaknya. Dengan menguasai rumus ini, kita dapat menyelesaikan masalah, membuat reka bentuk yang inovatif dan menghargai kerumitan dunia di sekeliling kita.
Rahsia simbol ajaib kuasai pembahagian di excel dengan mudah
Gaji paling tinggi di malaysia
Unveiling the enigma the tale of square root in the queens tongue