Smaschera le Disequazioni Algebriche: Risoluzione e Grafici a Prova di Bomba!
Avete presente quella sensazione di smarrimento totale quando si parla di algebra? Tranquille, siamo qui per questo! Oggi ci tuffiamo nel mondo delle disequazioni algebriche, quelle espressioni matematiche che sembrano fatte apposta per confonderci. Ma niente paura, con la nostra guida a prova di bomba, risolvere e rappresentare graficamente le disequazioni sarà un gioco da ragazze.
Immaginate di dover organizzare una festa: il numero di invitati può variare, ma avete un budget limitato. Le disequazioni algebriche ci aiutano a modellare situazioni come questa, trovando l'insieme di valori che soddisfano determinate condizioni, rappresentate dai simboli di disuguaglianza: maggiore di (>), minore di (<), maggiore o uguale a (≥), minore o uguale a (≤).
Le disequazioni algebriche affondano le loro radici nell'antica Mesopotamia, evolvendosi nel corso dei secoli grazie a matematici come Diofanto di Alessandria e Muhammad ibn Musa al-Khwarizmi. Oggi, questo strumento matematico è fondamentale in diversi ambiti, dall'economia all'ingegneria, dall'informatica alla fisica, permettendoci di analizzare dati, risolvere problemi di ottimizzazione e prendere decisioni informate.
Tuttavia, la strada verso la padronanza delle disequazioni algebriche può essere disseminata di ostacoli. Spesso ci si trova alle prese con errori di calcolo, difficoltà nel rappresentare graficamente le soluzioni o confusione nell'interpretare il significato dei risultati. Ma non temete, con un pizzico di pratica e la giusta dose di pazienza, potrete superare qualsiasi difficoltà e utilizzare le disequazioni algebriche a vostro vantaggio.
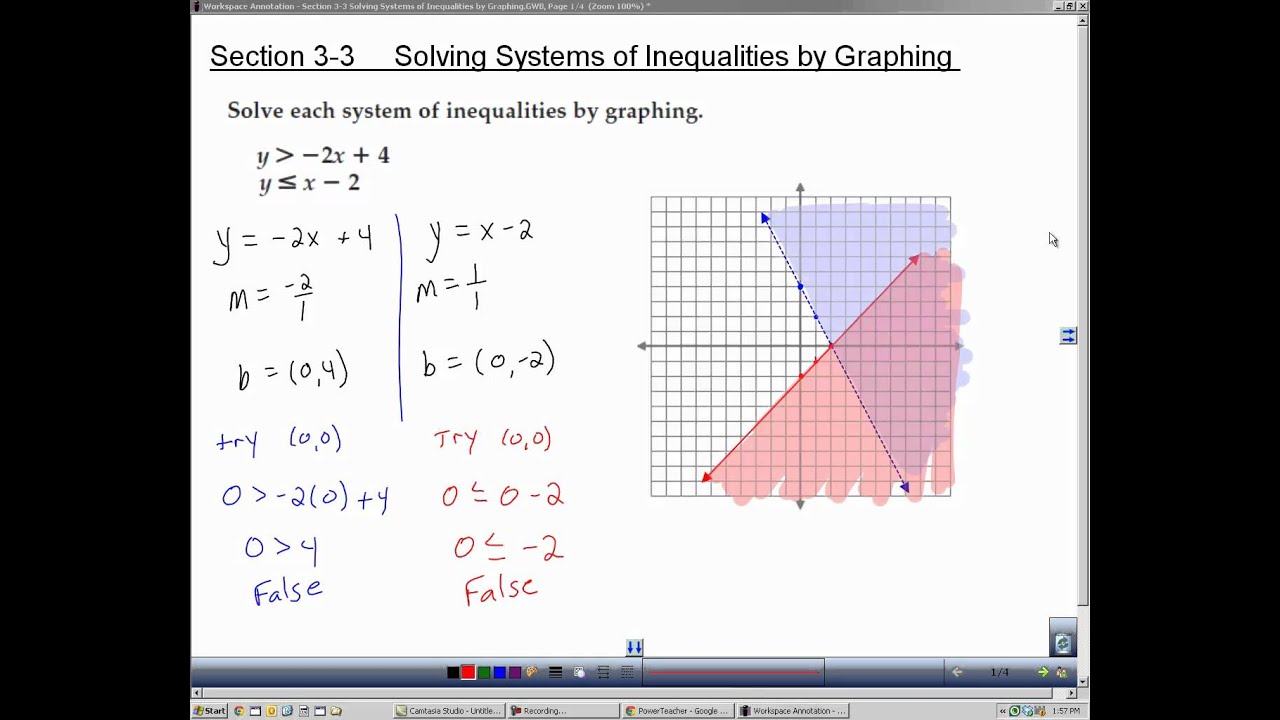
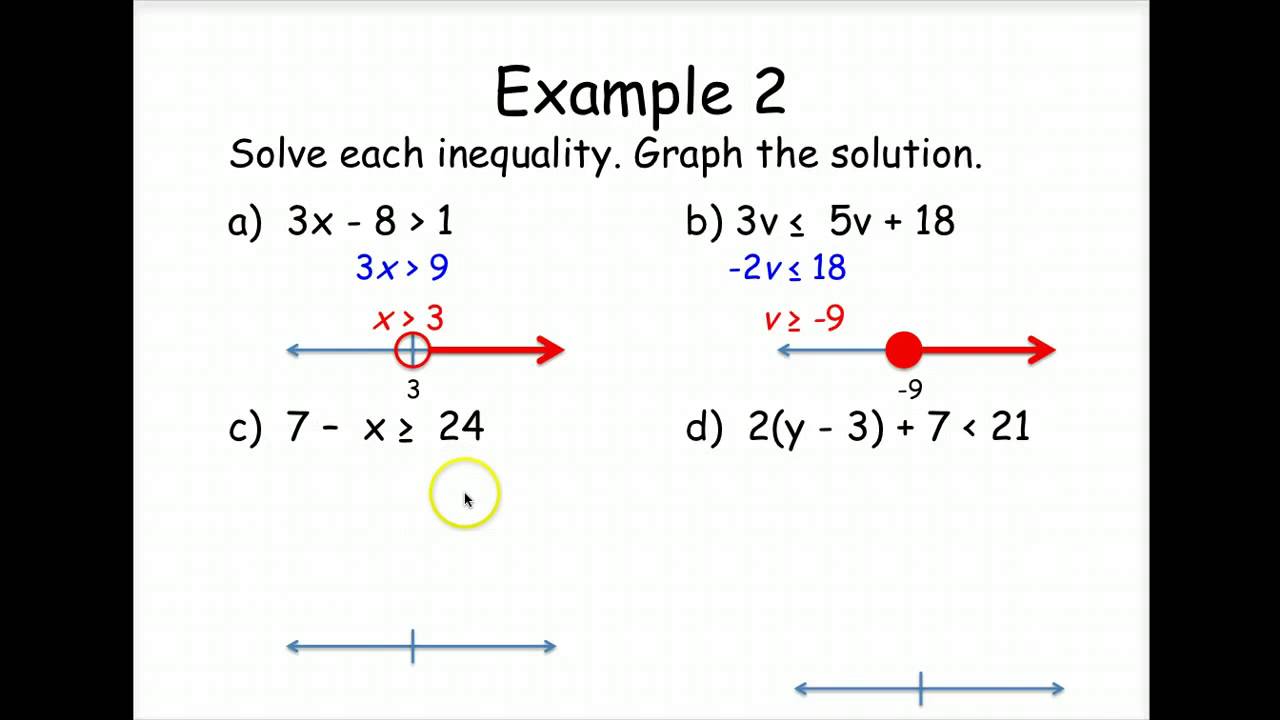
Per esempio, supponiamo di dover risolvere la disequazione 2x + 5 < 11. Il nostro obiettivo è isolare la variabile 'x'. Sottraendo 5 da entrambi i lati, otteniamo 2x < 6. Dividendo entrambi i lati per 2, troviamo x < 3. Questo significa che qualsiasi numero minore di 3 soddisfa la disequazione iniziale.
Rappresentare graficamente questa soluzione è semplice: basta tracciare una linea numerica e contrassegnare il punto 3 con un cerchio vuoto (perché 3 non è incluso nelle soluzioni) e ombreggiare la parte della linea a sinistra del 3, indicando tutti i valori di 'x' minori di 3.
Vantaggi e Svantaggi delle Disequazioni Algebriche
| Vantaggi | Svantaggi |
|---|---|
| Modellare situazioni reali complesse | Possibilità di errori di calcolo |
| Risolvere problemi di ottimizzazione | Difficoltà nella rappresentazione grafica di soluzioni complesse |
| Prendere decisioni informate in diversi ambiti | Interpretazione errata dei risultati |
Padroneggiare le disequazioni algebriche non è solo una questione di voti a scuola, ma un modo per affinare il pensiero critico e sviluppare capacità di problem-solving applicabili in diversi contesti. Con impegno e costanza, anche voi potrete aggiungere questo potente strumento al vostro arsenale matematico!
Progettazione italiano classe prima media la chiave per un apprendimento efficace
Scheda frutta e verdura guida completa per scelte sane
Documenti inps la guida completa per i datori di lavoro
