Maîtriser l'évaluation de la notion de fonction
Comprendre le concept de fonction est essentiel en mathématiques. Mais comment évaluer concrètement cette notion ? C'est une question fondamentale pour progresser et appliquer ce concept dans divers domaines. Cet article explore en profondeur l'évaluation de la notion de fonction, de sa définition à ses applications pratiques.
L'évaluation de la notion de fonction est un processus crucial qui permet de déterminer la valeur d'une fonction pour une entrée donnée. Cette compétence est au cœur de nombreux problèmes mathématiques et s'étend à des domaines comme la physique, l'informatique et l'économie. Sans une compréhension solide de ce processus, il est difficile d'appliquer efficacement les fonctions dans des contextes réels.
L'histoire de la notion de fonction remonte à plusieurs siècles, avec des contributions de mathématiciens renommés. Le concept a évolué au fil du temps, passant d'une simple relation entre des quantités à une définition plus formelle. L'importance de l'évaluation des fonctions est devenue de plus en plus évidente avec le développement de nouvelles branches des mathématiques et des sciences.
Un des problèmes principaux liés à l'évaluation de la notion de fonction est la confusion entre la fonction elle-même et sa valeur en un point donné. Il est essentiel de distinguer ces deux aspects pour éviter les erreurs d'interprétation. Un autre défi réside dans la maîtrise des différentes techniques d'évaluation, notamment pour les fonctions complexes ou composées.
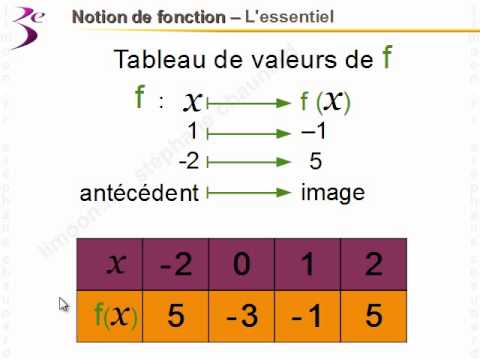
Une fonction peut être vue comme une machine qui transforme une entrée en une sortie. L'évaluation d'une fonction consiste à fournir une entrée spécifique à cette machine et à observer la sortie correspondante. Par exemple, si f(x) = 2x + 1, l'évaluation de f(3) consiste à remplacer x par 3, ce qui donne f(3) = 2*3 + 1 = 7.
L'évaluation précise des fonctions offre plusieurs avantages. Premièrement, elle permet de résoudre des problèmes concrets en modélisant des situations réelles avec des fonctions. Deuxièmement, elle facilite la compréhension du comportement des fonctions, notamment leurs variations et leurs limites. Troisièmement, elle est essentielle pour l'apprentissage de concepts mathématiques plus avancés, comme le calcul différentiel et intégral.
Pour évaluer une fonction, il faut suivre quelques étapes simples : identifier la fonction, remplacer la variable par la valeur donnée, puis effectuer les opérations nécessaires pour obtenir le résultat. Par exemple, pour évaluer g(x) = x² - 4 pour x = -2, on remplace x par -2 : g(-2) = (-2)² - 4 = 4 - 4 = 0.
Avantages et Inconvénients de l'évaluation de la notion de fonction
Bien que fondamentale, l'évaluation des fonctions présente certains défis. Par exemple, des erreurs de calcul peuvent survenir, notamment avec des fonctions complexes. Il est donc important de vérifier les résultats et d'utiliser des outils appropriés.
Questions fréquemment posées :
1. Qu'est-ce que l'évaluation d'une fonction ? Réponse : C'est le processus de détermination de la valeur d'une fonction pour une entrée donnée.
2. Pourquoi est-il important d'évaluer les fonctions ? Réponse : Pour résoudre des problèmes, comprendre le comportement des fonctions et progresser en mathématiques.
3. Comment évaluer une fonction composée ? Réponse : En évaluant d'abord la fonction interne, puis en utilisant le résultat comme entrée pour la fonction externe.
4. Quelles sont les erreurs courantes lors de l'évaluation des fonctions ? Réponse : Les erreurs de calcul, la confusion entre la fonction et sa valeur, et l'application incorrecte des règles d'opération.
5. Comment éviter les erreurs d'évaluation ? Réponse : En vérifiant les calculs, en utilisant des exemples concrets et en pratiquant régulièrement.
6. Quels outils peuvent aider à l'évaluation des fonctions ? Réponse : Les calculatrices, les logiciels de mathématiques et les ressources en ligne.
7. Comment interpréter le résultat de l'évaluation d'une fonction ? Réponse : En le reliant au contexte du problème et en analysant son impact sur le comportement de la fonction.
8. Où trouver des exercices d'évaluation de fonctions ? Réponse : Dans les manuels scolaires, les sites web éducatifs et les applications mobiles dédiées aux mathématiques.
En conclusion, l'évaluation de la notion de fonction est un pilier des mathématiques. Sa maîtrise est indispensable pour résoudre des problèmes, comprendre des concepts plus avancés et appliquer les mathématiques dans divers domaines. En pratiquant régulièrement et en utilisant les ressources disponibles, vous pouvez améliorer vos compétences en évaluation de fonctions et exploiter pleinement leur potentiel. N'hésitez pas à explorer davantage ce concept fondamental pour consolider vos bases mathématiques.
Anne with an e saison 2 episode 8 un tourbillon demotions a avonlea
Bicarbonate de soude un allie meconnu pour la sante animale
Redemarrez votre aventure retro lalternateur 2cv 12v neuf secret dune renaissance electrique