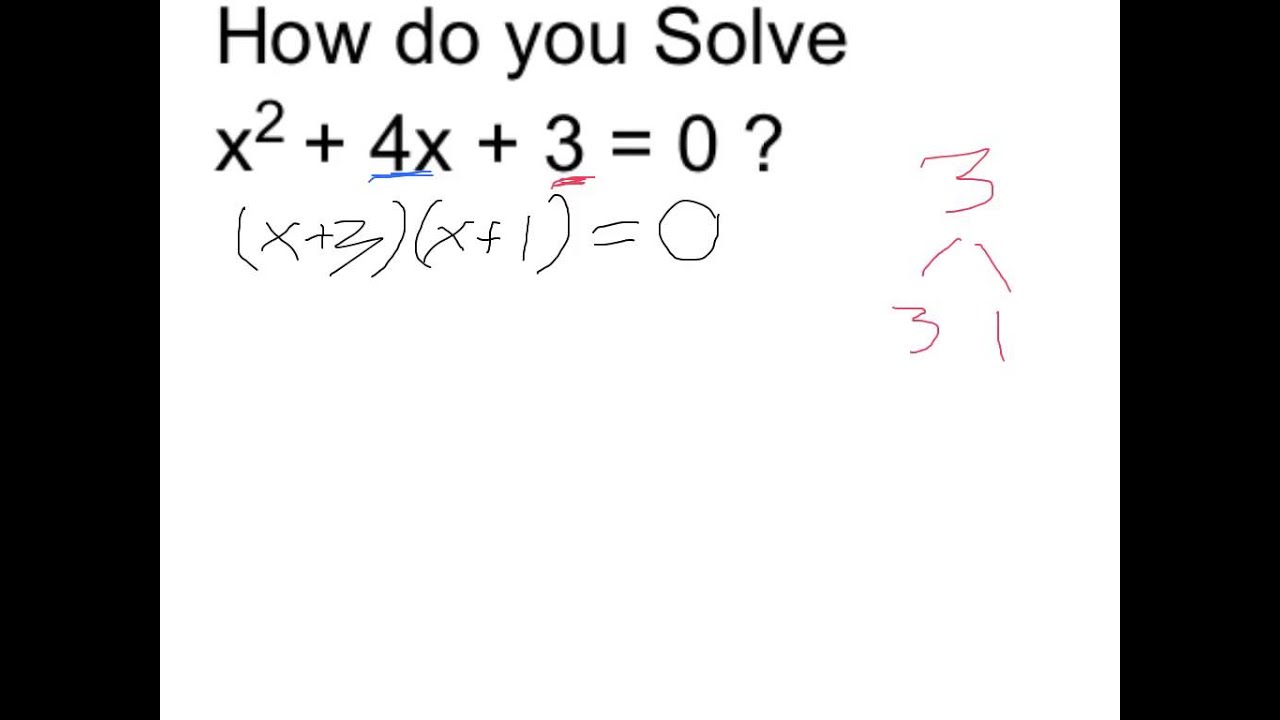Factoriser x²-4x : Le guide complet
Vous êtes-vous déjà demandé comment simplifier des expressions mathématiques qui semblent complexes à première vue ? La factorisation est une technique puissante qui permet de transformer des expressions algébriques en un produit de facteurs plus simples. Aujourd'hui, nous allons explorer comment factoriser l'expression x²-4x, un exemple fondamental qui illustre les principes de base de la factorisation.
La factorisation est une compétence essentielle en algèbre, elle permet de résoudre des équations, de simplifier des expressions et de comprendre la structure des polynômes. Maitriser la factorisation de x²-4x est une étape importante pour aborder des problèmes plus complexes en mathématiques.
L'histoire de la factorisation remonte à l'Antiquité, avec des traces de son utilisation dans les mathématiques babyloniennes et égyptiennes. Au fil des siècles, les mathématiciens ont développé des méthodes de plus en plus sophistiquées pour factoriser des expressions algébriques. Aujourd'hui, la factorisation est un outil essentiel dans de nombreux domaines, de la physique à l'informatique.
Un des problèmes courants rencontrés lors de la factorisation de x²-4x est l'oubli du facteur commun. Il est important de bien identifier tous les facteurs communs pour obtenir une factorisation complète et correcte.
Pour factoriser x²-4x, nous recherchons le facteur commun aux deux termes. Dans ce cas, le facteur commun est x. Nous pouvons donc écrire x²-4x comme x(x-4). C'est la forme factorisée de l'expression. Par exemple, si x = 5, x²-4x = 5²-4*5 = 25-20 = 5. Et x(x-4) = 5(5-4) = 5*1 = 5. Les deux expressions sont équivalentes.
Avantages de la factorisation de x²-4x :
1. Simplification : La forme factorisée x(x-4) est plus simple et plus facile à manipuler que la forme développée x²-4x.
2. Résolution d'équations : La factorisation permet de résoudre des équations du second degré. Par exemple, si x²-4x = 0, alors x(x-4) = 0, ce qui signifie que x = 0 ou x = 4.
3. Compréhension de la structure : La factorisation révèle la structure de l'expression et permet de mieux comprendre ses propriétés.
Guide étape par étape pour factoriser x²-4x :
1. Identifier le facteur commun : Dans ce cas, c'est x.
2. Factoriser le facteur commun : x(x-4).
FAQ :
1. Qu'est-ce que la factorisation ? La factorisation est le processus de décomposition d'une expression en un produit de facteurs.
2. Pourquoi factoriser x²-4x ? Pour simplifier l'expression et résoudre des équations.
3. Quel est le facteur commun de x² et -4x ? Le facteur commun est x.
4. Quelle est la forme factorisée de x²-4x ? La forme factorisée est x(x-4).
5. Comment vérifier la factorisation ? En développant la forme factorisée, on doit retrouver l'expression initiale.
6. Peut-on factoriser x²+4x ? Oui, on peut factoriser x²+4x comme x(x+4).
7. La factorisation est-elle toujours possible ? Non, certaines expressions ne peuvent pas être factorisées.
8. Où puis-je trouver plus d'informations sur la factorisation ? Des ressources en ligne et des manuels d'algèbre proposent des explications plus approfondies.
Conseils et astuces : Pour factoriser rapidement, identifiez toujours en premier le facteur commun le plus évident. N'oubliez pas de vérifier votre factorisation en développant l'expression obtenue.
En conclusion, la factorisation de x²-4x est une technique fondamentale en algèbre. Elle permet de simplifier des expressions, de résoudre des équations et de mieux comprendre la structure des polynômes. La forme factorisée x(x-4) est plus concise et plus facile à manipuler que la forme développée x²-4x. Maitriser cette technique est essentiel pour progresser en mathématiques et aborder des concepts plus avancés. N'hésitez pas à pratiquer la factorisation avec d'autres exemples pour consolider vos connaissances.
Travailler a distance sans limites on decrypte tout ca
Decouvrir le monde fascinant des tortues hermann
Reussir le grand ecart guide complet et conseils
