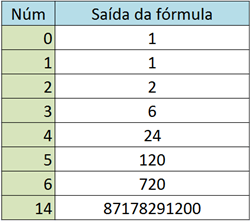
El factorial de cero: ¿Por qué 0! = 1?
El mundo de las matemáticas está lleno de conceptos intrigantes, y uno de ellos es el factorial. Si bien la mayoría puede calcular fácilmente el factorial de números enteros positivos, el factorial de cero a menudo genera confusión. ¿Por qué el factorial de cero es igual a 1? Esta pregunta ha intrigado a muchos estudiantes de matemáticas a lo largo de los años.
Para comprender el factorial de cero, primero debemos recordar qué es un factorial. En términos simples, el factorial de un número entero no negativo, denotado por el símbolo "!", es el producto de todos los enteros positivos menores o iguales a ese número. Por ejemplo, el factorial de 5 (5!) es 5 * 4 * 3 * 2 * 1 = 120.
Entonces, ¿dónde encaja el cero en esto? Si seguimos la definición de factorial, podríamos intentar calcular 0! como 0 * (0-1) * (0-2) * ... Sin embargo, esto nos lleva a una multiplicación infinita sin un resultado definido. Aquí es donde entra en juego la lógica matemática y las convenciones.
El factorial de cero se define como 1 por razones de consistencia y para mantener la utilidad del factorial en diferentes áreas de las matemáticas. Una forma de entender esto es a través de la función gamma, una generalización del factorial a números complejos. La función gamma se define de tal manera que su valor en 1 es 1, y para cualquier número complejo z, Γ(z+1) = zΓ(z). Usando esta relación recursiva y trabajando hacia atrás desde Γ(1) = 1, encontramos que Γ(0) = 1, lo que implica que 0! = 1.
Otra forma de ver esto es considerar el número de formas de ordenar un conjunto de objetos. Por ejemplo, hay 3! = 6 maneras de ordenar 3 objetos diferentes. Del mismo modo, solo hay una forma de ordenar un conjunto vacío (sin objetos), lo que significa que 0! = 1.
El factorial de cero es un concepto fundamental que aparece en muchas áreas de las matemáticas, incluyendo la combinatoria, el álgebra, el cálculo y la teoría de probabilidades. Su definición como 1 es crucial para la coherencia y la aplicabilidad de estas ramas matemáticas. Aunque pueda parecer contradictorio al principio, comprender la justificación matemática detrás de este concepto revela su elegancia y importancia en el mundo matemático.
A continuación, se presentan algunos ejemplos concretos de cómo se usa el factorial de cero en matemáticas:
- En combinatoria, el factorial de cero se utiliza para calcular el número de formas de elegir 0 objetos de un conjunto de n objetos, que siempre es 1 (no hay elección).
- En la expansión de la serie de Taylor, que se utiliza para representar funciones como sumas infinitas, el factorial de cero aparece en el término constante.
- En la fórmula de la distribución binomial, utilizada en probabilidad y estadística, el factorial de cero aparece al calcular la probabilidad de que un evento ocurra 0 veces en n ensayos.
Para concluir, el hecho de que el factorial de cero sea igual a 1 puede parecer extraño al principio, pero es una convención matemática necesaria y bien fundamentada. Su importancia radica en mantener la consistencia y la utilidad del factorial en diversas áreas de las matemáticas. Comprender este concepto no solo profundiza nuestra comprensión del factorial, sino que también abre la puerta a una apreciación más profunda de la belleza y la lógica que sustentan las matemáticas.
Dibujos de cohetes espaciales un viaje a la imaginacion
Sol y luna cabo un paraiso en baja california sur
Mantente informado los fines de semana con rtve telediario
