Desvelando la superficie lateral del cilindro: más que una simple forma
Imagina un rollo de papel de cocina. Ahora, imagina desenvolverlo con cuidado. La superficie que se despliega ante ti, plana y rectangular, es la superficie lateral del cilindro que formaba el rollo. Aunque parezca un concepto abstracto, la superficie lateral del cilindro está presente en muchísimos objetos de nuestro día a día, desde latas de refresco hasta tuberías. Entender su cálculo y propiedades no solo es crucial en matemáticas e ingeniería, sino que también nos permite apreciar la elegancia y eficiencia de esta forma geométrica en nuestro entorno.
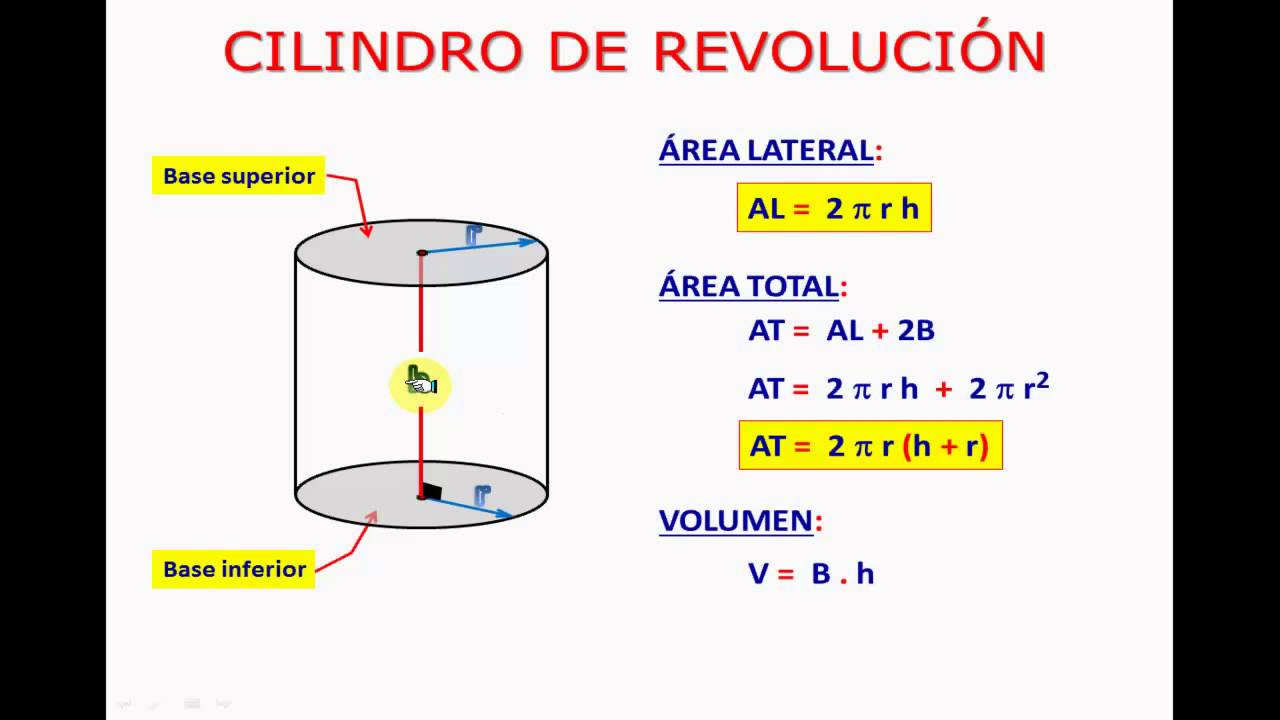
Pero, ¿qué es exactamente la superficie lateral del cilindro? En términos sencillos, es el área de la superficie curva que conecta las dos bases circulares del cilindro. Imaginemos que cortamos el rollo de papel de cocina a lo largo de su altura y lo extendemos. Obtendríamos un rectángulo cuya altura es la misma que la del cilindro, y cuya base es igual a la circunferencia del círculo que forma la base del cilindro.
La historia de la superficie lateral del cilindro se entrelaza con la del propio cilindro, una forma geométrica conocida desde la antigüedad. Los antiguos egipcios ya utilizaban cilindros en la construcción y en la vida cotidiana, y hay evidencias de que comprendían la relación entre la circunferencia, el diámetro y el área de los círculos, conocimientos esenciales para el cálculo de la superficie lateral del cilindro.
La fórmula para calcular la superficie lateral del cilindro es sorprendentemente simple: 2πrh, donde "r" es el radio de la base del cilindro y "h" es su altura. Esta fórmula se deduce fácilmente al visualizar el desarrollo de la superficie lateral del cilindro en un rectángulo, como mencionamos anteriormente. La base del rectángulo es la circunferencia del círculo (2πr) y su altura es la altura del cilindro (h).
Dominar el cálculo de la superficie lateral del cilindro es fundamental en diversas áreas. En ingeniería, por ejemplo, es esencial para diseñar envases eficientes, calcular la cantidad de material necesario para construir tuberías o determinar la resistencia al viento de estructuras cilíndricas. En matemáticas, el concepto de superficie lateral se extiende a otras figuras geométricas y sienta las bases para el cálculo de áreas y volúmenes más complejos.
A pesar de su aparente simplicidad, calcular la superficie lateral del cilindro puede presentar algunos desafíos. Uno de los errores más comunes es utilizar el diámetro del círculo en lugar del radio en la fórmula. También es importante asegurarse de que las unidades de medida sean consistentes para la altura y el radio.
Comprender la superficie lateral del cilindro nos ayuda a apreciar la eficiencia de esta forma en la naturaleza y en el diseño humano. Su capacidad para minimizar la superficie en relación con el volumen la convierte en una forma ideal para el almacenamiento de líquidos y gases, como lo vemos en las latas de refrescos y en los tanques de combustible. Además, la resistencia estructural del cilindro lo hace adecuado para la construcción de columnas, pilares y otras estructuras que soportan peso.
Ventajas y desventajas de utilizar objetos con forma de cilindro
| Ventajas | Desventajas |
|---|---|
| Eficiencia en el uso de materiales | Dificultad para apilar en algunas configuraciones |
| Resistencia estructural | Menor estabilidad en comparación con formas con bases más amplias |
| Facilidad de fabricación y transporte | Espacio vacío en el centro si se utiliza para almacenamiento |
Para concluir, aunque a simple vista la superficie lateral del cilindro pueda parecer un concepto meramente matemático, su comprensión nos abre las puertas a un mundo de aplicaciones y nos permite apreciar la elegancia y eficiencia de esta forma geométrica en nuestro entorno. Desde las latas de refresco hasta las complejas estructuras de ingeniería, la superficie lateral del cilindro está presente en innumerables aspectos de nuestra vida cotidiana, demostrando que la geometría no es solo una rama de las matemáticas, sino un lenguaje que nos ayuda a comprender y dar forma al mundo que nos rodea.
See you on tuesday mas que una simple despedida
Plantillas para flores de papel para imprimir
Golazo al futuro domina el temario primero de secundaria
