Stetigkeit und Differenzierbarkeit: Ein Irrglaube aufgeklärt
Ist jede stetige Funktion auch differenzierbar? Diese Frage führt oft zu Verwirrung und Missverständnissen in der Analysis. Der weit verbreitete Irrglaube, dass Stetigkeit automatisch Differenzierbarkeit impliziert, hält sich hartnäckig. Dieser Artikel klärt den Mythos auf und beleuchtet die tatsächliche Beziehung zwischen diesen beiden wichtigen Konzepten der Mathematik.
Stetigkeit beschreibt die Eigenschaft einer Funktion, keine Sprünge oder Lücken aufzuweisen. Anschaulich gesprochen lässt sich der Graph einer stetigen Funktion ohne Absetzen des Stiftes zeichnen. Differenzierbarkeit hingegen bezieht sich auf die Existenz der Ableitung einer Funktion an einem bestimmten Punkt. Die Ableitung gibt die momentane Änderungsrate der Funktion an und entspricht geometrisch der Steigung der Tangente an den Graphen.
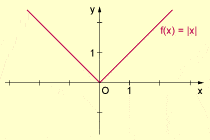
Die zentrale Aussage "Jede stetige Funktion ist differenzierbar" ist falsch. Es gibt zahlreiche Beispiele für Funktionen, die zwar stetig, aber nicht überall differenzierbar sind. Ein klassisches Beispiel ist die Betragsfunktion f(x) = |x|. Diese Funktion ist überall stetig, besitzt aber an der Stelle x = 0 keinen eindeutigen Tangentenanstieg und ist somit dort nicht differenzierbar.
Die Verwechslung entsteht möglicherweise durch die Tatsache, dass Differenzierbarkeit Stetigkeit impliziert. Anders ausgedrückt: Jede differenzierbare Funktion ist auch stetig. Die Umkehrung gilt jedoch nicht, wie das Beispiel der Betragsfunktion zeigt.
Das Verständnis der Beziehung zwischen Stetigkeit und Differenzierbarkeit ist fundamental für die Analysis und ihre Anwendungen in verschiedenen Bereichen wie Physik, Ingenieurwesen und Wirtschaft. Die korrekte Anwendung dieser Konzepte ist entscheidend für die Modellierung und Analyse von realen Prozessen.
Historisch gesehen wurden die Konzepte der Stetigkeit und Differenzierbarkeit im Laufe der Entwicklung der Infinitesimalrechnung präzisiert. Mathematiker wie Newton und Leibniz legten den Grundstein für diese Konzepte, die später von Cauchy und Weierstrass rigoros formalisiert wurden. Die Erkenntnis, dass Stetigkeit nicht Differenzierbarkeit impliziert, war ein wichtiger Schritt in der Entwicklung der Analysis.
Ein einfaches Beispiel für eine stetige, aber nicht differenzierbare Funktion ist die schon erwähnte Betragsfunktion f(x) = |x|. An der Stelle x = 0 bildet der Graph einen Knick, was die Existenz einer eindeutigen Tangente und somit der Ableitung verhindert.
Vor- und Nachteile des Verständnisses von Stetigkeit und Differenzierbarkeit
| Vorteile | Nachteile |
|---|---|
| Fundamentales Verständnis der Analysis | Abstraktes Konzept, erfordert mathematisches Verständnis |
| Anwendbar in vielen Bereichen der Wissenschaft und Technik | Kann zu Fehlinterpretationen führen, wenn nicht korrekt verstanden |
Häufig gestellte Fragen:
1. Ist jede differenzierbare Funktion stetig? Ja.
2. Ist jede stetige Funktion differenzierbar? Nein.
3. Was ist ein Beispiel für eine stetige, aber nicht differenzierbare Funktion? Die Betragsfunktion f(x) = |x|.
4. Was ist die Ableitung? Die momentane Änderungsrate einer Funktion.
5. Was ist Stetigkeit? Die Eigenschaft einer Funktion, keine Sprünge oder Lücken aufzuweisen.
6. Was ist Differenzierbarkeit? Die Existenz der Ableitung einer Funktion.
7. Wer hat die Grundlagen der Infinitesimalrechnung gelegt? Newton und Leibniz.
8. Was ist die geometrische Interpretation der Ableitung? Die Steigung der Tangente an den Graphen der Funktion.
Zusammenfassend lässt sich sagen, dass die Aussage "Jede stetige Funktion ist differenzierbar" falsch ist. Stetigkeit ist eine notwendige, aber keine hinreichende Bedingung für Differenzierbarkeit. Das Verständnis dieses Unterschieds ist entscheidend für den erfolgreichen Umgang mit den Konzepten der Analysis. Die Fähigkeit, stetige und differenzierbare Funktionen zu identifizieren und zu analysieren, ist unerlässlich für Anwendungen in verschiedenen wissenschaftlichen und technischen Disziplinen. Ein tieferes Verständnis dieses Themas ermöglicht es, komplexe mathematische Modelle zu entwickeln und zu interpretieren und somit ein besseres Verständnis der Welt um uns herum zu gewinnen. Vertiefen Sie Ihr Wissen über dieses Thema, indem Sie Lehrbücher der Analysis konsultieren und Online-Ressourcen nutzen, um Ihr Verständnis zu erweitern und Ihre mathematischen Fähigkeiten zu verbessern.
Bilder paw patrol zum ausdrucken
Herz uber kopf spruche geburtstag ein widerspruch
Window color vorlagen meer tauche ein in die unterwasserwelt
