Die Kunst der Differenzierbarkeit: Wann ist eine Funktion differenzierbar?
Stellen Sie sich eine geschwungene Linie vor. Können Sie an jedem Punkt eine Tangente anlegen? Diese Frage führt uns direkt zum Kern der Differentialrechnung: Wann ist eine Funktion differenzierbar? Die Antwort ist grundlegend für das Verständnis vieler Bereiche der Mathematik, Physik und Ingenieurwissenschaften.
Die Differenzierbarkeit einer Funktion beschreibt ihre "Glattheit". Eine differenzierbare Funktion hat an jeder Stelle eine definierte Ableitung, was bedeutet, dass sie keine Knicke, Sprünge oder Lücken aufweist. Die Ableitung gibt die momentane Änderungsrate der Funktion an und ermöglicht es uns, das Verhalten der Funktion präzise zu analysieren.
Die Frage nach der Differenzierbarkeit ist eng mit dem Begriff des Grenzwerts verbunden. Eine Funktion ist an einem Punkt differenzierbar, wenn der Grenzwert des Differenzenquotienten an diesem Punkt existiert. Dieser Grenzwert repräsentiert die Steigung der Tangente an die Funktion in diesem Punkt.
Das Konzept der Differenzierbarkeit geht auf Gottfried Wilhelm Leibniz und Isaac Newton zurück, die im 17. Jahrhundert unabhängig voneinander die Grundlagen der Differentialrechnung entwickelten. Die Notwendigkeit, physikalische Phänomene, wie die Bewegung von Objekten, genau zu beschreiben, trieb die Entwicklung dieses wichtigen mathematischen Werkzeugs voran.
Die Bedeutung der Differenzierbarkeit liegt in ihrer Anwendung in vielen Bereichen. Von der Optimierung in der Wirtschaft bis zur Modellierung von physikalischen Prozessen – die Differenzierbarkeit ermöglicht es uns, komplexe Systeme zu analysieren und vorherzusagen.
Eine Funktion ist an einem Punkt x₀ differenzierbar, wenn der Grenzwert des Differenzenquotienten für h gegen Null existiert. Formal ausgedrückt: f'(x₀) = lim (h->0) [f(x₀ + h) - f(x₀)] / h. Dieser Grenzwert, falls er existiert, ist die Ableitung der Funktion an der Stelle x₀.
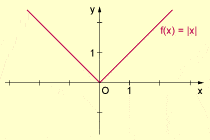
Ein einfaches Beispiel: Die Funktion f(x) = x² ist überall differenzierbar. Ihre Ableitung ist f'(x) = 2x. Die Funktion f(x) = |x| (Betragsfunktion) hingegen ist an der Stelle x = 0 nicht differenzierbar, da dort ein Knick vorliegt und somit keine eindeutige Tangente definiert werden kann.
Vorteile der Differenzierbarkeit:
1. Berechnung der momentanen Änderungsrate: Ermöglicht die Analyse von Wachstums- und Zerfallsprozessen.
2. Optimierung: Ermöglicht die Bestimmung von Maxima und Minima von Funktionen, z.B. zur Gewinnmaximierung.
3. Modellierung physikalischer Prozesse: Beschreibung von Geschwindigkeit, Beschleunigung und anderen physikalischen Größen.
Häufig gestellte Fragen:
1. Was ist der Unterschied zwischen Stetigkeit und Differenzierbarkeit? Antwort: Jede differenzierbare Funktion ist stetig, aber nicht jede stetige Funktion ist differenzierbar.
2. Was bedeutet es, wenn die zweite Ableitung Null ist? Antwort: Ein möglicher Wendepunkt.
3. Kann eine Funktion an einem Punkt differenzierbar sein, aber nicht stetig? Antwort: Nein.
4. Was ist ein kritischer Punkt? Antwort: Ein Punkt, an dem die Ableitung Null oder undefiniert ist.
5. Wie berechnet man die Ableitung einer Funktion? Antwort: Mit Hilfe der Ableitungsregeln.
6. Was ist die geometrische Interpretation der Ableitung? Antwort: Die Steigung der Tangente.
7. Was ist die Bedeutung der Differenzierbarkeit in der Physik? Antwort: Beschreibung von Bewegungsabläufen.
8. Wie kann man die Differenzierbarkeit einer Funktion überprüfen? Antwort: Durch Anwendung der Definition des Grenzwerts des Differenzenquotienten.
Tipps und Tricks: Üben Sie das Berechnen von Ableitungen mit verschiedenen Funktionen. Visualisieren Sie die Funktion und ihre Tangente, um die Differenzierbarkeit besser zu verstehen.
Zusammenfassend lässt sich sagen, dass die Differenzierbarkeit einer Funktion ein Schlüsselkonzept in der Analysis ist. Sie ermöglicht die Berechnung der momentanen Änderungsrate und spielt eine entscheidende Rolle in der Optimierung und Modellierung. Das Verständnis der Bedingungen für Differenzierbarkeit ist daher unerlässlich für ein tieferes Verständnis mathematischer und physikalischer Zusammenhänge. Vertiefen Sie Ihr Wissen durch weitere Übungen und Anwendungen, um die volle Kraft der Differentialrechnung zu erschließen.
Lustige bilder wochenende in sicht so startet man mit humor ins wochenende
Den nachsten bruckentag clever planen tipps tricks fur maximale freizeit
Bild news aktuell heute deutschland was sie wissen mussen
