Das Geheimnis der 45-45-90 Regel: Geometrisches Wissen clever nutzen
Stellen Sie sich vor, Sie könnten komplexe geometrische Probleme mit einem einfachen Trick lösen. Die 45-45-90 Regel bietet genau das! Sie ist ein mächtiges Werkzeug, das Berechnungen in bestimmten rechtwinkligen Dreiecken deutlich vereinfacht. Doch was steckt eigentlich hinter dieser geheimnisvollen Regel?
Die 45-45-90 Regel, auch bekannt als Satz des Pythagoras für spezielle rechtwinklige Dreiecke, beschreibt die Seitenverhältnisse in einem rechtwinkligen Dreieck mit zwei gleich großen Winkeln von 45 Grad. Dieses spezielle Dreieck, auch gleichschenklig-rechtwinkliges Dreieck genannt, taucht in vielen Bereichen der Mathematik, Architektur und sogar im Alltag auf.
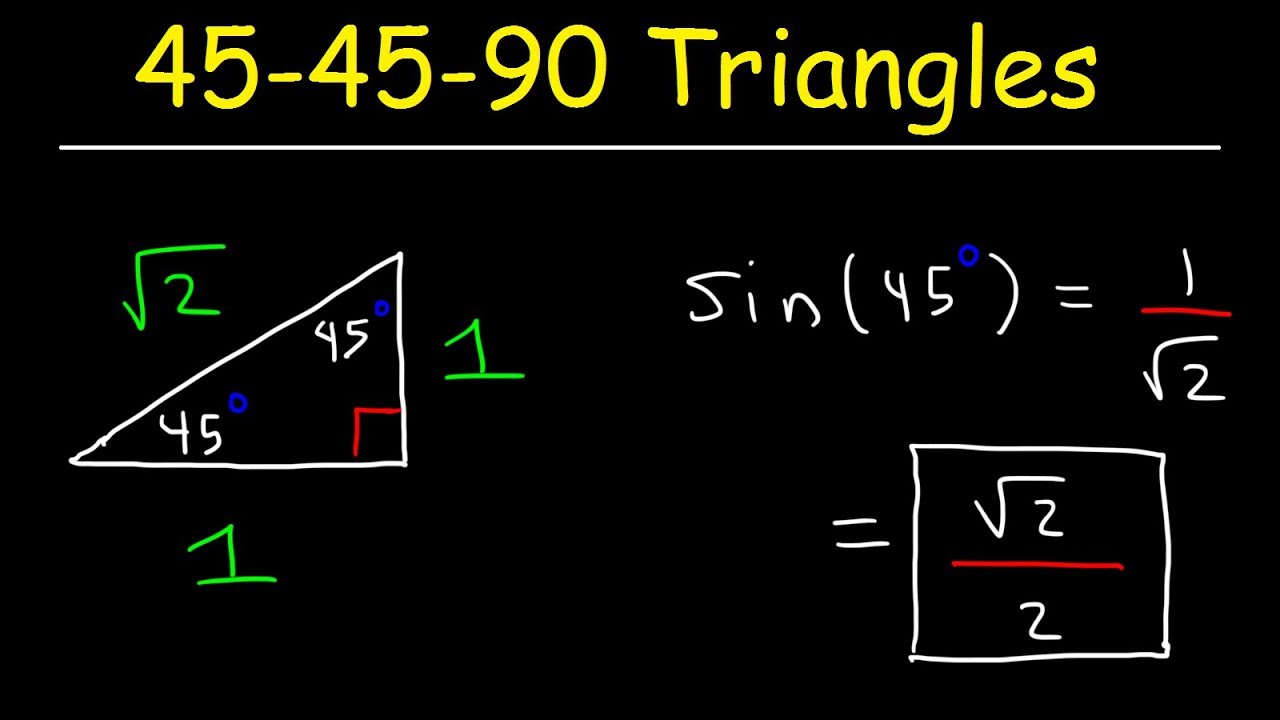
Die Regel besagt, dass die beiden Katheten gleich lang sind und die Hypotenuse das √2-fache der Kathetenlänge beträgt. Diese einfache Beziehung ermöglicht es uns, unbekannte Seitenlängen schnell und effizient zu berechnen, ohne komplizierte Formeln anwenden zu müssen.
Die Kenntnis dieser Regel ist nicht nur für Schüler und Studenten relevant, sondern auch für alle, die mit geometrischen Formen arbeiten. Ob beim Planen eines Bauprojekts, beim Entwerfen eines Möbelstücks oder beim Berechnen von Winkeln und Distanzen – die 45-45-90 Regel kann wertvolle Zeit und Mühe sparen.
In diesem Artikel tauchen wir tief in die Welt der 45-45-90 Regel ein. Wir erforschen ihre Geschichte, ihre Bedeutung und ihre vielfältigen Anwendungsmöglichkeiten. Bereiten Sie sich darauf vor, die Geheimnisse dieses faszinierenden geometrischen Konzepts zu lüften!
Die 45-45-90 Regel lässt sich direkt aus dem Satz des Pythagoras ableiten. Da die Katheten gleich lang sind (nennen wir die Länge a), gilt für die Hypotenuse c: c² = a² + a² = 2a². Daraus folgt c = a√2. Die Geschichte dieser Regel ist eng mit der Entdeckung des Satz des Pythagoras und der Erforschung von rechtwinkligen Dreiecken verbunden, die bis in die antike babylonische Mathematik zurückreicht.
Ein einfaches Beispiel: Hat eine Kathete die Länge 5 cm, so ist die andere Kathete ebenfalls 5 cm lang und die Hypotenuse beträgt 5√2 cm.
Vorteile der 45-45-90 Regel:
1. Vereinfachte Berechnungen: Die Regel ermöglicht schnelles Berechnen der Seitenlängen im 45-45-90 Dreieck.
2. Zeitersparnis: Komplexe Berechnungen mit dem Satz des Pythagoras entfallen.
3. Praktische Anwendung: Nützlich in vielen Bereichen wie Architektur, Design und Konstruktion.
Aktionsplan: Identifizieren Sie ein 45-45-90 Dreieck. Messen Sie eine Seite. Berechnen Sie die anderen Seiten mit der 45-45-90 Regel.
Vor- und Nachteile der 45-45-90 Regel
| Vorteile | Nachteile |
|---|---|
| Einfache Anwendung | Nur für 45-45-90 Dreiecke gültig |
| Schnelle Berechnungen |
Häufig gestellte Fragen:
1. Was ist die 45-45-90 Regel? Antwort: Die Seitenverhältnisse in einem gleichschenklig-rechtwinkligen Dreieck.
2. Wie lautet die Formel? Antwort: Kathete * √2 = Hypotenuse
3. Wo wird sie angewendet? Antwort: Architektur, Design, Mathematik.
4. Ist sie mit dem Satz des Pythagoras verwandt? Antwort: Ja, sie leitet sich daraus ab.
5. Wie berechnet man die Kathete, wenn die Hypotenuse bekannt ist? Antwort: Hypotenuse / √2 = Kathete
6. Was ist ein gleichschenklig-rechtwinkliges Dreieck? Antwort: Ein Dreieck mit zwei gleichen Winkeln (45°) und einem rechten Winkel.
7. Kann man die Regel auch bei anderen Dreiecken anwenden? Antwort: Nein, nur bei 45-45-90 Dreiecken.
8. Gibt es Online-Rechner für die 45-45-90 Regel? Antwort: Ja, diverse Webseiten bieten solche Rechner an.
Tipp: Merken Sie sich die Verhältniszahl √2 für die Hypotenuse!
Zusammenfassend lässt sich sagen, dass die 45-45-90 Regel ein mächtiges Werkzeug in der Geometrie ist. Sie vereinfacht Berechnungen in gleichschenklig-rechtwinkligen Dreiecken erheblich und findet Anwendung in vielen Bereichen, von der Architektur bis zur Mathematik. Die Kenntnis dieser Regel spart Zeit und Mühe und ermöglicht ein tieferes Verständnis geometrischer Zusammenhänge. Nutzen Sie die 45-45-90 Regel, um geometrische Probleme effizient zu lösen und Ihre mathematischen Fähigkeiten zu verbessern. Beginnen Sie noch heute, die Vorteile dieser einfachen, aber effektiven Regel zu entdecken und vertiefen Sie Ihr Wissen mit den zahlreichen Online-Ressourcen, die Ihnen zur Verfügung stehen. Die 45-45-90 Regel ist ein wertvolles Werkzeug für jeden, der mit Geometrie arbeitet, und ihr Verständnis öffnet Türen zu einem besseren Verständnis mathematischer Prinzipien.
Legendare metal bands die grossten ikonen des heavy metal
Ausmalbilder weihnachten micky maus weihnachtszauber zum ausmalen
Geometrie knacken klasse 8 losungsstrategien und ubungen